

我正在尝试创建一个简单的基于深度学习的模型来预测y=x**2但是看起来深度学习无法在其训练集范围之外学习一般功能。
直观地说,我可以认为神经网络可能无法拟合y=x**2,因为输入之间没有乘法。
请注意,我不是在问如何创建适合x**2的模型。我已经做到了。我想知道以下问题的答案:
完成笔记本的路径:https://github.com/krishansubudhi/MyPracticeProjects/blob/master/KerasBasic-nonlinear.ipynb
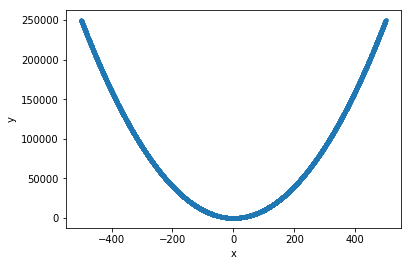
培训投入:
x = np.random.random((10000,1))*1000-500
y = x**2
x_train= x
训练码
def getSequentialModel():
model = Sequential()
model.add(layers.Dense(8, kernel_regularizer=regularizers.l2(0.001), activation='relu', input_shape = (1,)))
model.add(layers.Dense(1))
print(model.summary())
return model
def runmodel(model):
model.compile(optimizer=optimizers.rmsprop(lr=0.01),loss='mse')
from keras.callbacks import EarlyStopping
early_stopping_monitor = EarlyStopping(patience=5)
h = model.fit(x_train,y,validation_split=0.2,
epochs= 300,
batch_size=32,
verbose=False,
callbacks=[early_stopping_monitor])
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_18 (Dense) (None, 8) 16
_________________________________________________________________
dense_19 (Dense) (None, 1) 9
=================================================================
Total params: 25
Trainable params: 25
Non-trainable params: 0
_________________________________________________________________
随机测试集上的评估
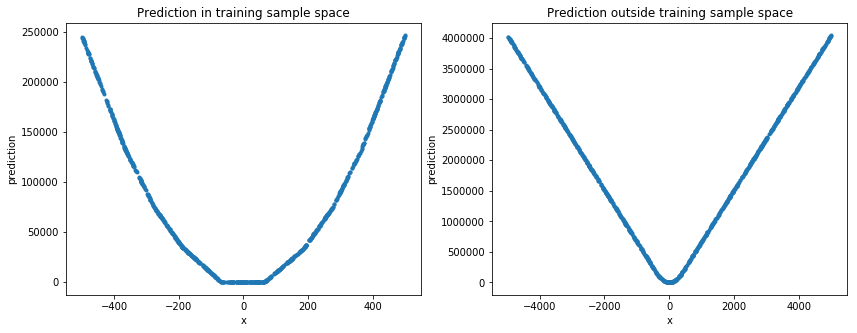
这个例子中的深度学习并不擅长预测一个简单的非线性函数;而是擅长预测训练数据样本空间中的值。
鉴于我在评论中说你的网络肯定不深,让我们接受你的分析确实是正确的(毕竟,你的模型在其训练范围内似乎确实做得很好),以便进入你的第二个问题,这是有趣的问题。
嗯,这种问题不完全适合SO,因为“非常有限”的确切含义可以说不清楚…
因此,让我们尝试重新表述它:我们是否应该期望DL模型在它们被训练的数值域之外预测这样的数值函数?
来自不同领域的一个例子可能在这里有所启发:假设我们已经建立了一个能够检测到
这么说吧答案很明确
我们人类很容易认为这样的模型应该能够外推,尤其是在数字领域,因为这是我们自己非常“容易”做的事情;但是ML模型,虽然非常擅长插值,但它们在外推任务中失败得很惨,比如你在这里提出的任务。
为了让它更直观,认为这些模型的整个“世界”都局限在它们的训练集中:我上面的示例模型将能够泛化和识别看不见的照片中的动物,只要这些动物在训练中“介于”(注意引号);以类似的方式,你的模型在预测你用于训练的样本之间的参数的函数值方面做得很好。但是在这两种情况下,这些模型都不会超出它们的训练域(即外推)。除了动物之外,我的示例模型没有“世界”,同样,对于超过[-500,500]的模型…
如需佐证,请考虑DeepMind最近的论文神经算术逻辑单元;引用摘要:
神经网络可以学习表示和操作数值信息,但它们很少在训练过程中遇到的数值范围之外很好地泛化。
另见一位著名从业者的相关推文:
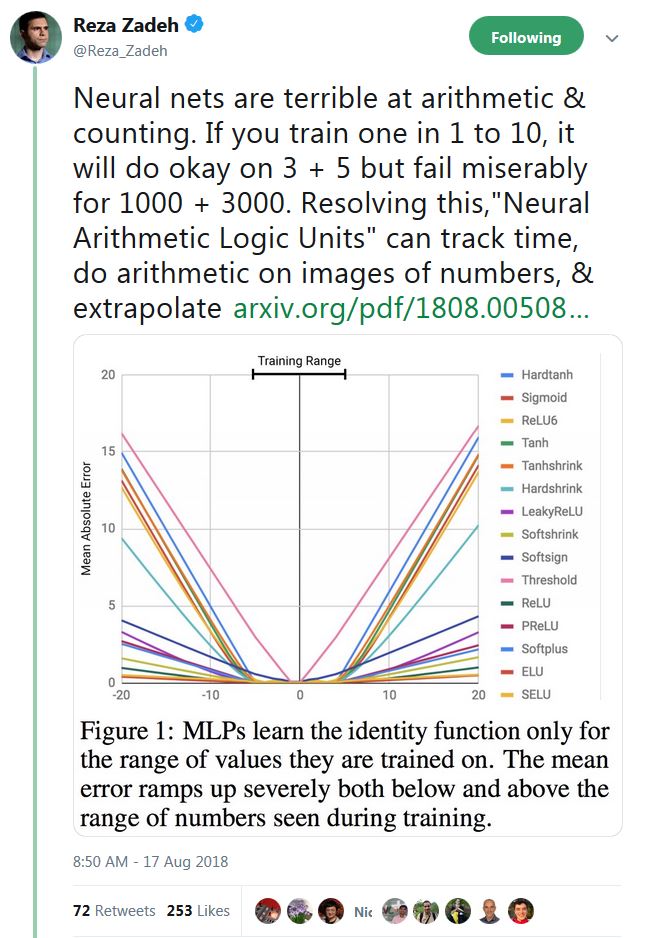
关于你的第三个问题:
现在应该很清楚,这是当前研究的一个(热门)领域;首先,请参阅上面的论文…
那么,深度学习模型有限吗?当然——在可预见的未来,忘记关于AGI的可怕故事。正如你所说,它们非常有限吗?嗯,我不知道…但是,考虑到它们在推断方面的局限性,它们有用吗?
这可以说是真正感兴趣的问题,答案显然是——见鬼,是的!