我对大型稀疏矩阵的Cholesky分解感兴趣。我遇到的问题是，Cholesky因子不一定是稀疏的（就像两个稀疏矩阵的乘积不一定是稀疏的）。

例如，对于仅沿第一行，第一列和对角线具有非零的矩阵，Cholesky因子具有100%的填充（下三角形和上三角形是100%的密度）。在下面的图像中，灰色为非零，而白色为零。

我知道的一个解决方案是，找到一个置换P矩阵，然后对psupt/supap进行Cholesky分解。例如，对于相同的矩阵，通过应用将第一行移动到最后一行，将第一列移动到最后一列的置换矩阵，Cholesky因子是稀疏的。

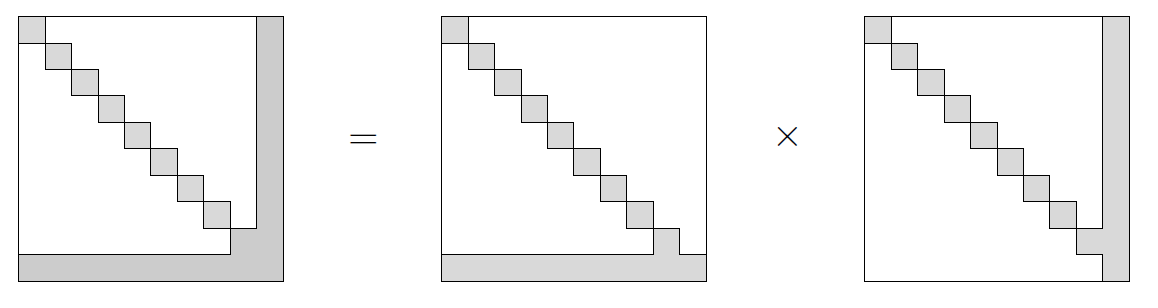
我的问题是一般如何确定P？

要从一个更真实的矩阵中了解A和PSUPT/SUPAP的Cholesky分解的区别，请看下面的图像。我从http://www.seas.ucla.edu/vandenbe/103/lectures/chol.pdf上获取了所有这些图像

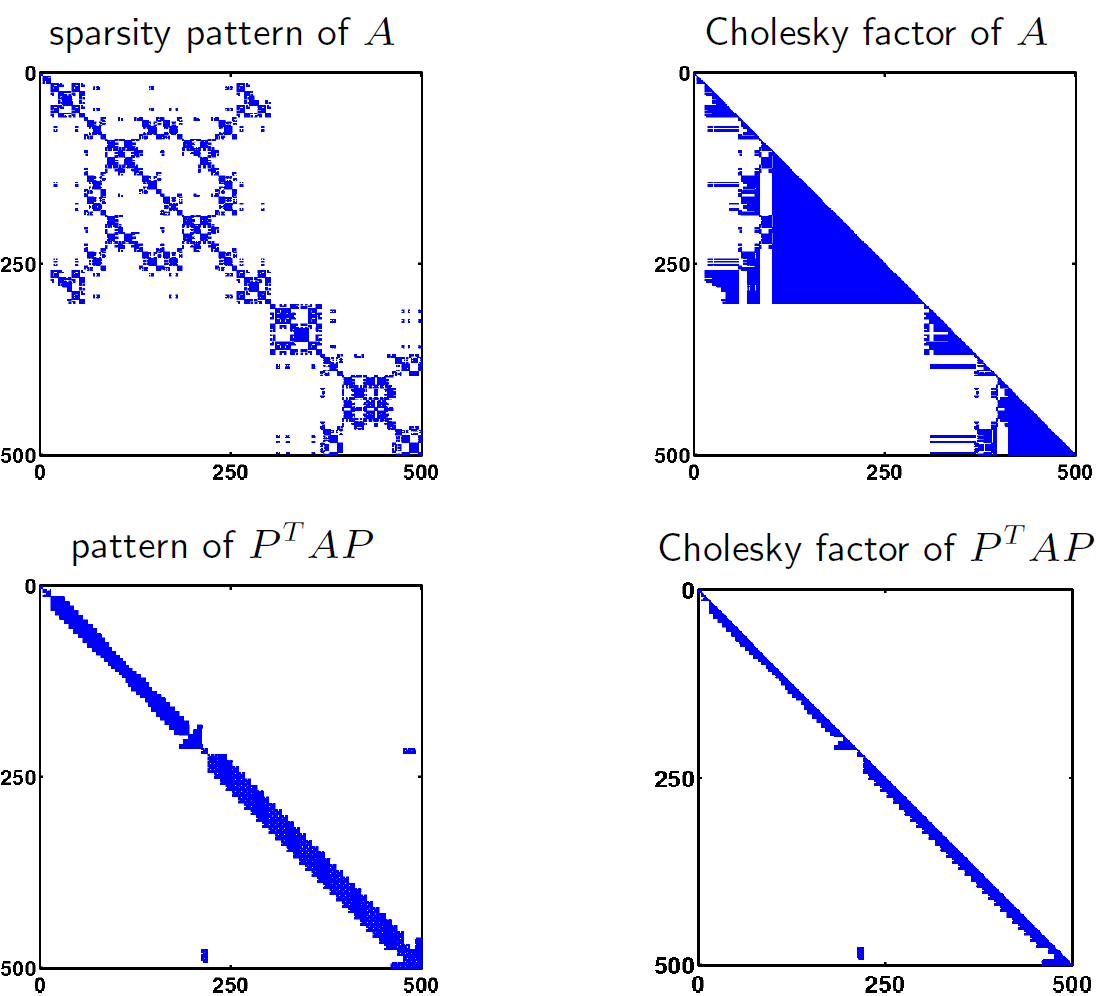
根据课堂讲稿

有许多启发式方法（我们没有讨论）来选择好的置换矩阵P。

我想知道其中的一些方法是什么（用C，C++，甚至Java编写的代码会是理想的）。