

我如何做的宽度优先搜索遍历的skLearning决策树?
在我的代码中,我尝试了sklearn。tree_uu库,并使用了各种函数,如tree_uuu。特征和树结构。了解树结构的阈值。但是这些函数执行dfs树遍历如果我想执行bfs,我应该怎么做?
假设一下
clf1 = DecisionTreeClassifier( max_depth = 2 )
clf1 = clf1.fit(x_train, y_train)
这是我的分类器,生成的决策树是

然后,我使用以下函数遍历了树
def encoding(clf, features):
l1 = list()
l2 = list()
for i in range(len(clf.tree_.feature)):
if(clf.tree_.feature[i]>=0):
l1.append( features[clf.tree_.feature[i]])
l2.append(clf.tree_.threshold[i])
else:
l1.append(None)
print(np.max(clf.tree_.value))
l2.append(np.argmax(clf.tree_.value[i]))
l = [l1 , l2]
return np.array(l)
生产的产品是
数组([['address',age',None,None,'age',None,None],[0.5,17.5,2,1,1,15.5,1,1]],dtype=object),其中第一个数组是节点的特征,或者如果它是叶节点,则它被标记为None,第二个数组是特征节点的阈值,对于类节点,它是类,但这是树的dfs遍历我想做bfs遍历,我该怎么做?以上部分已经回答。
我想知道我们是否可以将树存储到数组中,使其看起来像是一个完整的二叉树,以便第i个节点的子节点存储在2i 1 th和2i 2 th索引?
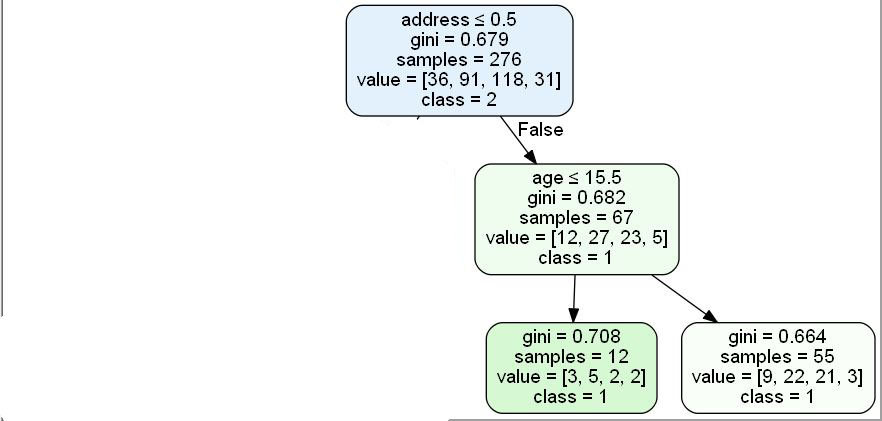
对于上面的树,生成的输出是数组([['address','age',None,None],[0.5,15.5,1,1]],dtype=object)
但是想要的输出是
数组([['address',None',age',None,None,None,None],[0.5,-1,15.5,-1,-1,1,1]],dtype=object)
若第一个数组中的值为无,第二个数组中的值为-1,则表示该节点不存在。在这里,地址的右子代age位于数组的2*02=2索引处,类似地,age的左子代和右子代分别位于数组的2*21=5索引和2*22=6索引处。
像这样的?
def reformat_tree(clf):
tree = clf.tree_
feature_out = np.full((2 ** tree.max_depth), -1, dtype=tree.feature.dtype)
threshold_out = np.zeros((2 ** tree.max_depth), dtype=tree.threshold.dtype)
stack = []
stack.append((0, 0))
while stack:
current_node, new_node = stack.pop()
feature_out[new_node] = tree.feature[current_node]
threshold_out[new_node] = tree.threshold[current_node]
left_child = tree.children_left[current_node]
if left_child >= 0:
stack.append((left_child, 2 * current_node + 1))
right_child = tree.children_right[current_node]
if right_child >= 0:
stack.append((right_child, 2 * current_node + 2))
return feature_out, threshold_out
我无法在你的树上测试它,因为你还没有给出复制它的方法,但它应该可以工作。
该函数以所需的格式返回特征和阈值。特征值为-1的节点是不存在的,而-2的节点是叶子。
这是通过遍历树并跟踪当前位置来实现的。