

我尝试在JavaScript中实现Dijkstra的最短路径算法,并用多个示例对其进行了测试。
我正在使用此图来查看它的行为:
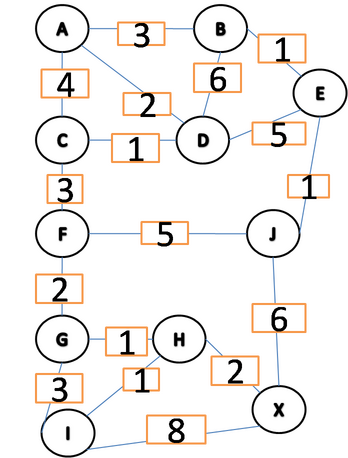
如果我想找到从A到I的最短路径,结果应该是距离等于10的[A, D,C,F,G,H,I]。
但是我的实现返回路径为[A, B,E,J,F,G,H,I],距离为14。
这是我的JavaScript代码:
const graph = {
A: {B: 3, C: 4, D: 2},
B: {A: 3, D: 6, E: 1},
C: {A: 4, D: 1, F: 3},
D: {A: 2, B: 6, C: 1, E: 5},
E: {B: 1, D: 5, J: 1},
F: {C: 3, G: 2, J: 5},
G: {F: 2, H: 1, I: 3},
H: {G: 1, I: 1, X: 2},
I: {G: 3, H: 1, X: 8},
J: {E: 1, F: 5, X: 6},
X: {H: 2, I: 8, J: 6},
};
// The class Dsp:
class Dsp {
constructor() {
//Previous node after update of distance
this.prev = {};
//Distances of each node
this.distances = {};
//Array of unvisited neighbors
this.unvisitedn = [];
//Path of visited nodes from first to final node
this.path = [];
}
findsp(graph, start, end) {
//Register graph data
this.registerGraphData(graph, start);
//Set the starting node as the current node
let cn = start;
//While there are unvisited nodes
while (this.unvisitedn.length > 0) {
//Mark the currentNode as visited
this.markAsVisited(cn);
//Compare distance from current node to unvisited neighbors
let nodes = this.compareNodeDistances(graph, cn);
//Update neighbor distance
this.updateNodeDistances(nodes, cn);
//Compare each unvisited neighbor and choose the one with the lowest distances
//Set the choosed node as the new current node
cn = this.selectNextNode(graph, cn);
}
return this.generatePath(start, end);
}
registerGraphData(graph, start) {
//Set starting weight for all nodes
const higherWeight = 10000;
//For each node in the graph
for (let node in graph) {
//If the node is the starting node
if (node == start)
//Set starting weight as 0
this.distances[node] = 0;
//else set the higherWeight
else
this.distances[node] = higherWeight;
//Add to the unvisited nodes
this.unvisitedn.push(node);
}
console.log(this.distances);
console.log(this.unvisitedn);
}
markAsVisited(cn) {
console.log('Visiting', cn);
let index = this.unvisitedn.indexOf(cn);
this.unvisitedn.splice(index, 1);
}
getUnvisitedNeighbors(graph, cn) {
//All current node neighbors
let nbs = graph[cn];
let unbs = [];
for (let nb in nbs) {
if (this.unvisitedn.includes(nb))
unbs.push(nb);
}
console.log(cn, 'Unvisited neighbors:', unbs);
return unbs;
}
compareNodeDistances(graph, cn) {
let unbs = this.getUnvisitedNeighbors(graph, cn);
//new distances
let newDistances = {};
//For all currentNode neighbors
for (let nb of unbs) { //Substituted unbs
//Neighbor Weight
let nbw = graph[cn][nb];
//console.log('Neighbor weight', nbw);
//neighbor distance
let nbd = this.distances[nb];
//console.log('Neighbor distance', nbd);
//current node distance
let cnd = this.distances[cn];
//console.log('Current node distance', cnd);
//If the neighbor distance > current node distance + neighbor weight
if (nbd > cnd + nbw)
newDistances[nb] = cnd + nbw;
}
console.log('new distances:', newDistances);
return newDistances;
}
updateNodeDistances(nodes, cn) {
//Update distances for each neighbor that was compared
for (let node in nodes) {
console.log(nodes);
this.distances[node] = nodes[node];
this.prev[node] = cn;
}
console.log("Node distances after update", this.distances);
console.log("Node previous nodes after update", this.prev);
}
selectNextNode(graph, cn) {
let unbs = this.getUnvisitedNeighbors(graph, cn);
let mind = 100000;
let nextn = null;
//If there are unvisited neighbors
if (unbs.length > 0) {
for (let nb of unbs) {
if (this.distances[nb] < mind) {
mind = this.distances[nb];
nextn = nb;
}
}
} else {
nextn = this.unvisitedn[0];
}
return nextn;
}
generatePath(start, end) {
let cn = end;
let path = {};
let nodes = [];
while (cn !== start) {
nodes.push(cn);
cn = this.prev[cn];
}
nodes.push(start);
nodes.reverse();
path['nodes'] = nodes;
path['distance'] = this.distances[end];
return path;
}
}
let shp = new Dsp();
console.log(shp.findsp(graph, 'A', 'I'));我想了解我编程的步骤有什么问题。
我做错了什么?有什么额外的步骤或考虑吗?
问题是您没有执行最佳优先搜索。您的代码实际上执行了深度优先搜索,您只需优化您将从当前节点中选择哪个未访问的邻居。但是您应该从所有未访问节点中获取距离最小的节点,而不仅仅是当前节点的邻居。
参见维基百科上算法描述的第6步:
所以问题出在selectNextNode中。它可以更正为:
selectNextNode(graph, cn) {
let mindist = Infinity;
let best;
for (let node of this.unvisitedn) {
if (this.distances[node] < mindist) {
mindist = this.distances[node];
best = node;
}
}
return best;
}
然而,这是一个天真的实现,因为在每一轮中你必须再次找到最小值:这使得算法是非最优的。真正的Dijkstra算法将使用优先级队列,例如堆,这使得这种查找更加高效。
不幸的是,JavaScript(还)没有提供本机堆实现,所以我们必须抛出自己的或引用一个库。我从我的答案中提取了实现Javascript中实现优先级队列的有效方式?。有关该实现的更多详细信息,请参阅此处。
我认为最短路径算法的实现不保证使用类。像你的findsp这样的函数应该就足够了。
所以这里是:
/* MinHeap minimised - taken from https://stackoverflow.com/a/66511107/5459839 */
const MinHeap={siftDown(h,i=0,v=h[i]){if(i<h.length){let k=v[0];while(1){let j=i*2+1;if(j+1<h.length&&h[j][0]>h[j+1][0])j++;if(j>=h.length||k<=h[j][0])break;h[i]=h[j];i=j;}h[i]=v}},heapify(h){for(let i=h.length>>1;i--;)this.siftDown(h,i);return h},pop(h){return this.exchange(h,h.pop())},exchange(h,v){if(!h.length)return v;let w=h[0];this.siftDown(h,0,v);return w},push(h,v){let k=v[0],i=h.length,j;while((j=(i-1)>>1)>=0&&k<h[j][0]){h[i]=h[j];i=j}h[i]=v;return h}};
function DijkstraShortestPath(graph, start, end) {
// Heap with one entry: distance is 0 at start, and there is no previous.
let heap = [[0, start, null]];
let prev = {};
while (heap.length) {
let [distance, current, cameFrom] = MinHeap.pop(heap);
if (current in prev) continue; // Already visited
prev[current] = cameFrom; // Mark as visited
if (current == end) { // Found!
// Reconstruct path
let path = [];
while (current) {
path.push(current);
current = prev[current];
}
path.reverse();
return { path, distance };
}
// Push unvisited neighbors on the heap
for (let [neighbor, edge] of Object.entries(graph[current])) {
if (!(neighbor in prev)) MinHeap.push(heap, [distance + edge, neighbor, current]);
}
}
}
// Demo:
const graph = {
A: {B: 3, C: 4, D: 2},
B: {A: 3, D: 6, E: 1},
C: {A: 4, D: 1, F: 3},
D: {A: 2, B: 6, C: 1, E: 5},
E: {B: 1, D: 5, J: 1},
F: {C: 3, G: 2, J: 5},
G: {F: 2, H: 1, I: 3},
H: {G: 1, I: 1, X: 2},
I: {G: 3, H: 1, X: 8},
J: {E: 1, F: 5, X: 6},
X: {H: 2, I: 8, J: 6},
}
console.log(DijkstraShortestPath(graph, 'A', 'I'));
嗨,试试Dijkstra Algo的这段代码
const top = 0;
const parent = (i) => ((i + 1) >>> 1) - 1;
const left = (i) => (i << 1) + 1;
const right = (i) => (i + 1) << 1;
let g = new Array(100005);
let vis = new Array(100005);
class PriorityQueue {
constructor(comparator = (a, b) => a[0] < b[0]) {
this._heap = [];
this._comparator = comparator;
}
size() {
return this._heap.length;
}
isEmpty() {
return this.size() == 0;
}
peek() {
return this._heap[top];
}
push(...values) {
values.forEach((value) => {
this._heap.push(value);
this._siftUp();
});
return this.size();
}
pop() {
const poppedValue = this.peek();
const bottom = this.size() - 1;
if (bottom > top) {
this._swap(top, bottom);
}
this._heap.pop();
this._siftDown();
return poppedValue;
}
replace(value) {
const replacedValue = this.peek();
this._heap[top] = value;
this._siftDown();
return replacedValue;
}
_greater(i, j) {
return this._comparator(this._heap[i], this._heap[j]);
}
_swap(i, j) {
[this._heap[i], this._heap[j]] = [this._heap[j], this._heap[i]];
}
_siftUp() {
let node = this.size() - 1;
while (node > top && this._greater(node, parent(node))) {
this._swap(node, parent(node));
node = parent(node);
}
}
_siftDown() {
let node = top;
while (
(left(node) < this.size() && this._greater(left(node), node)) ||
(right(node) < this.size() && this._greater(right(node), node))
) {
let maxChild =
right(node) < this.size() && this._greater(right(node), left(node))
? right(node)
: left(node);
this._swap(node, maxChild);
node = maxChild;
}
}
}
function clean(n) {
for (let i = 0; i <= n; ++i) {
g[i] = [];
console.log(g);
vis[i] = 0;
console.log(vis);
}
}
function make_graph(edges) {
for (let i = 0; i < edges.length; i++) {
let it = edges[i];
let x = it[0];
let y = it[1];
let w = it[2];
g[x].push([w, y]);
g[y].push([w, x]);
}
}
// module.exports =
// //param A : integer
// //param B : array of array of integers
// //param C : integer
// //return a array of integers
function solve(n, edges, source) {
clean(n);
make_graph(edges);
let distance = new Array(n).fill(Infinity);
let q = new PriorityQueue();
distance[source] = 0;
q.push([0, source]);
while (q.size() > 0) {
let p = q.pop();
let x = p[1];
if (vis[x] == 1) continue;
vis[x] = 1;
for (let i = 0; i < g[x].length; ++i) {
let y = g[x][i][1];
let w = g[x][i][0];
if (distance[x] + w < distance[y]) {
distance[y] = distance[x] + w;
q.push([distance[y], y]);
}
}
}
for (let i = 0; i < n; ++i) {
if (distance[i] == Infinity) distance[i] = -1;
}
return distance;
}
let A = 6;
let B = [
[0, 4, 9],
[3, 4, 6],
[1, 2, 1],
[2, 5, 1],
[2, 4, 5],
[0, 3, 7],
[0, 1, 1],
[4, 5, 7],
[0, 5, 1],
];
let C = 4;
console.log(solve(A, B, C));