我的挑战是在另一个矩形内旋转一个矩形。

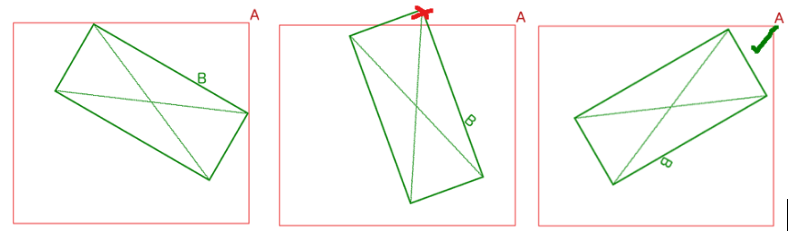
内部矩形，我们称之为B，不允许穿过外部矩形，我们称之为A。但是如果A进一步旋转，以便它可能再次到达合法位置，它应该被旋转到它。所以想要的行为是在它越过边界之前停止旋转，并在B再次具有合法位置时继续旋转。B是用鼠标旋转的，可能不是每一个度数都额外计算。所以鼠标事件可能指向20度，在下一次迭代中指向40度。

我的方法是通过计算和使用旋转来解决这个问题。我得到了指向鼠标的alpha旋转。Beta是从alpha到B的右上角的旋转。我计算了边界球（橙色）及其与A的碰撞点（左上角，右上角，右上角，右下角（左和Bot没有提到，以免使问题复杂化）。

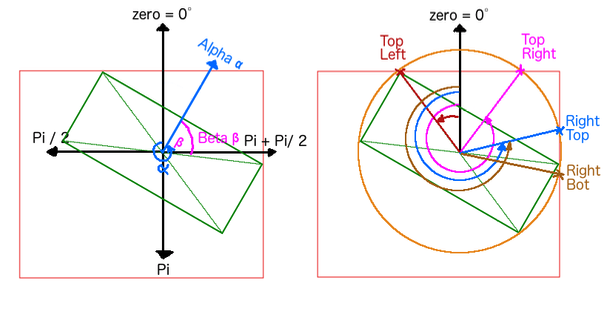
通过这种方法，我设法计算出何时必须停止，但仅限于顶部和右侧分开。例如：顺时针旋转-

If (B.leftTopCornerRotation < TopLeft ||  B.leftTopCornerRotation > TopRight) {
    Alpha = TopLeft - Beta;
} else if (B.leftBotCornerRotation < TopLeft ||  B. leftBotCornerRotation > TopRight) {
    Alpha = Topleft + Beta  + PI; // + PI rotates the value by 180 degree
} else if (B.rightBotCornerRotation < TopLeft ||  B. rightBotCornerRotation > TopRight) {
    Alpha = TopLeft - Beta + PI;
} else if (B.rightTopCornerRotation < TopLeft ||  B. rightTopCornerRotation > TopRight) {
    Alpha = TopLeft + Beta;
}

我的第一个问题是，如果B在不止一条线上出界（例如顶部和右侧），我会纠正旋转，这样右侧就没有越界，而不是纠正顶部没有越界。但是第二次纠正会导致右侧越界。这将导致一个无限循环。

我的第二个问题是，这种方法接缝真的很复杂。

我的问题是，如果有更好的/有效的方法来计算顺时针和逆时针方向的有效旋转，这样它就不会越过边界。最好的情况是它看起来像停在拐角处。