

这是相当复杂的解释,所以我会尽我所能,对不起,如果有什么我错过了,让我知道,我会纠正它。
我的问题是,我的任务是画这个形状,

这将使用C编写代码来计算此形状上的点。
重要细节。
用户输入-中心点(X, Y)、要显示的点数、字体大小(影响半径)
输出-形状上的坐标列表。
一旦我有了这些点,总体目标是将它们放入Excel上的图表中,它有望以用户输入的大小为我绘制它!
我知道最大半径是165毫米,最小半径是35毫米。我决定我的基本字体大小应该是20。然后我做了一些思考,想出了这个等式。
半径=(所选字体大小/20)*130。这只是一个估计,我意识到它可能不正确,但我认为它至少可以作为一个模板。
然后我决定我应该创建两个不同的圆,有两个不同的中心点,然后将它们连接在一起来创建形状。我认为内线必须有一个更大的半径和一个沿着X轴更远的中心点(Y保持不变),因为这样它就可以切入外线。
所以我将第二中心点定义为(X4,Y)。(同样,只是估计,认为它们相距多远并不重要)。
然后我决定半径2=(选择字体大小/20)*165(最大半径)
所以,我有两个半径和两个中心点。
现在要计算圆上的点,我真的很挣扎。我决定最好的方法是创建一个增量(这里是模板)
for(int i=0; i<=n; i++) //where 'n' is users chosen number of points
{
//Equation for X point
//Equation for Y Point
cout<<"("<<X<<","<<Y<<")"<<endl;
}
现在,对于我的生活,我不能找出一个方程来计算这些点。我已经找到了涉及角度的方程,但是因为我没有,我正在挣扎。
我想的另一点可能是一个问题是对计算的值施加限制,以仅显示形状上的值。?不知道如何选择限制,而不是使外线成为一个完整的半圆,这样我就有了一个最大半径?
那么。有人有任何提示/提示/链接可以与我分享如何准确进行吗?
再次感谢,任何问题的问题,对不起,如果你让我知道,我会尽力纠正。
干杯
更新;
R1 = (Font/20)*130;
R2 = (Font/20)*165;
for(X1=0; X1<=n; X1++)
{
Y1 = ((2*Y)+(pow(((4*((pow((X1-X), 2)))+(pow(R1, 2)))), 0.5)))/2;
Y2 = ((2*Y)-(pow(((4*((pow((X1-X), 2)))+(pow(R1, 2)))), 0.5)))/2;
cout<<"("<<X1<<","<<Y1<<")";
cout<<"("<<X1<<","<<Y2<<")";
}
意见?
根据Code-Guru对这个问题的评论,内圈看起来比外圈更像半圆。使用Code-Guru答案中的等式来计算内圈的点。然后,看看这个问题,如何计算一个与你的圆相交的圆的半径,给定距离(你可以任意设置)和交点(你知道,因为它是半圆)。从这个角度,你可以画出任何给定距离的外弧,你需要做的就是改变距离,直到你产生一个你满意的形状。
这个问题可能会帮助您应用Code-Guru的等式。
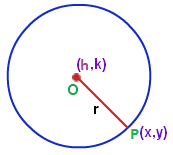
圆的方程是
(x - h)^2 + (y - k)^2 = r^2
用一点代数,您可以在从h到h r的范围内迭代x,递增一些适当的delta并计算y的两个相应值。这将绘制一个完整的圆。
下一步是找到两个圆相交的x坐标(假设月亮形状由两个合适的圆定义)。同样,一些代数和铅笔和纸会有所帮助。
更多详情:
要在不使用极坐标和三角的情况下绘制圆,您可以这样做:
for x in h-r to h+r increment by delta
calculate both y coordinates
要计算y坐标,您需要求解y的圆方程。最简单的方法是将其转换为形式为A*y^2 B*y C=0的二次方程,并使用二次方程:
(x - h)^2 + (y - k)^2 = r^2
(x - h)^2 + (y - k)^2 - r^2 = 0
(y^2 - 2*k*y + k^2) + (x - h)^2 - r^2 = 0
y^2 - 2*k*y + (k^2 + (x - h)^2 - r^2) = 0
所以我们有
A = 1
B = -2*k
C = k^2 + (x - h)^2 - r^2
现在将这些插入二次方程,并在for循环中为每个x值插入两个y值。(很可能,您将希望在一个或多个单独的函数中进行计算。)
正如你所看到的,这是相当混乱的。用三角学和角度来做这件事会干净得多。
更多想法:
即使问题中描述的用户输入中没有角度,也没有内在的原因不能在计算中使用它们(除非你有特定的要求,比如因为你的老师告诉你不要这样做)。话虽如此,使用极坐标使这变得更加容易。对于一个完整的圆,你可以这样做:
for theta = 0 to 2*PI increment by delta
x = r * cos(theta)
y = r * sin(theta)
要绘制一个圆弧,而不是一个完整的圆,您只需在for循环中更改theta的限制。例如,圆的左半部分从PI/2变为3*PI/2。