

我正在努力解决一个3D问题,我试图找到一个有效的算法。
我有一个给定宽度、高度和深度的边界框。
我还有一个球体列表。也就是说,每个球体的中心坐标(xi, yi,zi)和半径ri。
球体保证适合边界框内,并且不会相互重叠。
所以我的情况是这样的:
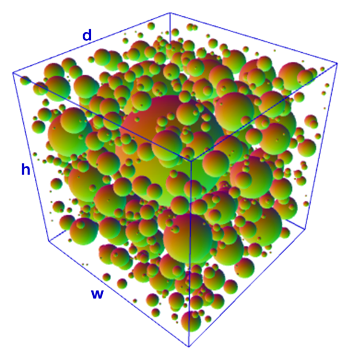
现在我有一个半径为r的新球体,我必须将其放入边界框中,而不是重叠任何先前的球体。
我也有一个目标点T=(x, y,z),我的目标是使这个新球体(给定上述条件)尽可能接近这个目标点。
我试图构造一个有效的算法来为新球体找到一个最佳位置。最佳的是:尽可能靠近目标点。或者如果在边界框内的任何地方,现有球体之间或周围没有空间来适应这个新球体,则为“错误”结果。
我想过各种复杂的方法,比如构建剩余体积的某种参数描述,从边界框开始,一个接一个地减去现有的球体。但这似乎并没有引导我找到可行的解决方案。
请注意,有很多已知的“球体打包”算法,但它们倾向于用随机球体填充卷。他们也经常使用试错方法,只做一定数量的随机尝试,然后终止。
而我有一个给定的新球体大小,我需要适应它(或者发现它是不可能的)。
一种可能的方法是通过计算球体的“距离图”,即为每个点(x,y,z)返回到最近球体的距离的函数,该距离也是到最近中心的距离减去相应球体的半径。地图由(超)锥形表面的交点组成。
然后您可以探索目标点周围的距离图,并找到值超过目标半径的最近点。
如果我是对的,距离图与球心(https://en.wikipedia.org/wiki/Weighted_Voronoi_diagram)的加权Voronoi图直接相关,图的顶点对应于局部极大值。因此,值超过目标半径的最近Voronoi顶点将给出一个解。
不幸的是,这个图的构造不会是一桶笑声。查看文章“3D球的欧几里得沃罗诺伊图及其通过跟踪边缘的计算”及其参考书目。
估计距离图的一个可能可行的解决方案是通过在规则的立方体网格中离散空间,并为每个立方体获得距离函数的下界和上界。
对于单个给定的球体和给定的立方体,可以通过分析找到最小值和最大值。然后考虑所有球体,你可以找到最小最大值和最小最小值,它们是真实距离的上界和下界(最大最小值不行)。然后你保持所有球体,使最小值保持在上界以下,你会得到一个(希望是简短的)候选列表。
在这里,您可以检查到列表中球体的距离,如果上界小于目标半径,您可以丢弃立方体。如果您在目标半径上方找到上界,则已找到解决方案。否则,如果距离函数上的不确定性范围太大,请将立方体细分为更小的立方体,以便更准确地估计上界和下界。
要获得接近目标点的解决方案,您将通过增加与目标的距离(使用嵌套数字球)来访问立方体,直到找到匹配项。
这个过程的一个关键点是快速找到最接近给定立方体的球体,以进行初始估计。像kD-tree或类似的数据结构可能会有所帮助。