

我需要编写一个程序来输入一个数字并以以下形式输出其阶乘的素数分解:
4!=(2^3)*(3^1)
5!=(2^3)*(3^1)*(5^1)
问题是我仍然无法弄清楚如何获得该结果。
显然,括号中的每个第一个数字都是升序素数,直到实际的阶乘。括号中的第二个数字是该数字在阶乘中出现的次数。
我无法弄清楚的是例如在 5!=(2^3)*(3^1)*(5^1)中,2 如何只出现 3 次,3 只出现 1 次,5 只出现一次 120 次 (5!=120)。
多亏了发表评论的乐于助人的人,我现在已经解决了这个问题,但我现在很难弄清楚如何在不实际计算阶乘的情况下获取数字并以这种格式获得阶乘。
每个数字都可以由素数的唯一(直到重新排序)乘法表示,称为数字的素因数分解,因为您正在寻找可以唯一创建该数字的素因数。
2^3=8
3^1=3
5^1=5
和 8*3*5=120
但这也意味着:(2^3)*(3^1)*(5^1) = 120
这并不是说 2 在数字 120 中作为数字出现 3 次,显然没有,而是将 2 乘以 2 乘以 2,总共 3 个 2。3 和 5 也是如此,它们在 120 的素数分解中出现一次。你提到的表达式向你展示了数字 120 的这种独特的素数分解。这是在 Python 中获取数字素数分解的一种方法:
def pf(number):
factors=[]
d=2
while(number>1):
while(number%d==0):
factors.append(d)
number=number/d
d+=1
return factors
运行它,你会得到:
>>> pf(120)
[2, 2, 2, 3, 5]
如上所述,乘以得到 120。这里有一个小图表可以更清楚地说明这一点:
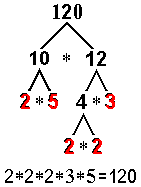
考虑例如 33!它是以下产品的产物:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
这些因素是:
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2
2 2 2 2
2 2
2
3 3 3 3 3 3 3 3 3 3 3
3 3 3
3
5 5 5 5 5 5
5
7 7 7 7
11 11 11
13 13
17
19
23
29 31
你看到模式了吗?
33! = 2^( 33 div 2 + 33 div 4 + 33 div 8 + 33 div 16 + 33 div 32) *
3^( 33 div 3 + 33 div 9 + 33 div 27) *
5^( 33 div 5 + 33 div 25) *
----
7^( 33 div 7) * 11^( 33 div 11) * 13^( 33 div 13) *
----
17 * 19 * 23 * 29 * 31
因此,要找到 n! 的素数分解,而不做任何乘法或因式分解,我们只需要有不大于 n 的素数有序列表,我们分三个阶段处理(重复整数除法和可能的求和)- 小于或等于 n 平方根的素数;小于或等于 n/2;其余的。
实际上,使用惰性评估,它甚至比这更简单。假设素数已经实现,按顺序返回素数流,在 Haskell 中,阶乘分解为
ff n = [(p, sum . takeWhile (> 0) . tail . iterate (`div` p) $ n)
| p <- takeWhile (<= n) primes]
-- Prelude> ff 33
-- [(2,31),(3,15),(5,7),(7,4),(11,3),(13,2),(17,1),(19,1),(23,1),(29,1),(31,1)]
因为 33 div 4 是 (33 div 2) div 2,依此类推。
2^3 是写 23 或 2 的另一种方式。(2^3)(3^1)(5^1) = 2 3× 3 × 5 = 120。
(2^3)(3^1)(5^1) 只是用纯 ASCII 文本表示的 120 的质因式分解,而不是用漂亮的数学格式表示。您的作业需要以这种形式输出,仅仅是因为您比弄清楚如何输出格式化方程式更容易输出(并且可能是因为它更容易处理评分)。
这里用于以纯文本表示方程的约定足够标准,您可以直接将此文本键入 google.com 或 wolframalpha.com,它将为您计算结果为 120:(2^3)(3^1)(5^1) 在 wolframalpha.com / (2^3)(3^1)(5^1) 在 google.com
WolframAlpha 还可以计算素因数分解, 您可以使用它来获取测试结果以与您的程序进行比较.例如:1000的质因数分解!
实际计算阶乘的朴素解决方案将仅处理最多 12 的数字(如果使用 32 位整数)。这是因为13!为 ~62 亿,大于 32 位 int 中可以表示的最大数字。
但是,如果您避免先计算阶乘,则可以处理更大的输入。我不会确切地告诉你如何做到这一点,因为要么弄清楚它是你作业的一部分,要么你可以问你的教授/助教。但以下是一些提示。
a b × a c = a b c
等式 (a)
10 × 15 = (2 1 × 5 1) × (3 1 × 5 1) = 2 1 × 3 1 × (5 1 × 5 1) = 2 1 × 3 1 × 5 2 如
您所见,计算 10 × 15 的素数分解无需将 10 乘以 15;您可以改为计算各个项的素因数分解,然后组合这些因式分解。