

我正在使用pyomo来找到解决能源最佳化问题的方法。我试图在一天中找到最佳的时间段来将智能洗碗机的启动时间转移到,这样电费成本就最小化了。
我正在使用一篇论文中的一个例子,但不幸的是,我还不能嵌入图片,所以这里是描述问题的图片链接:
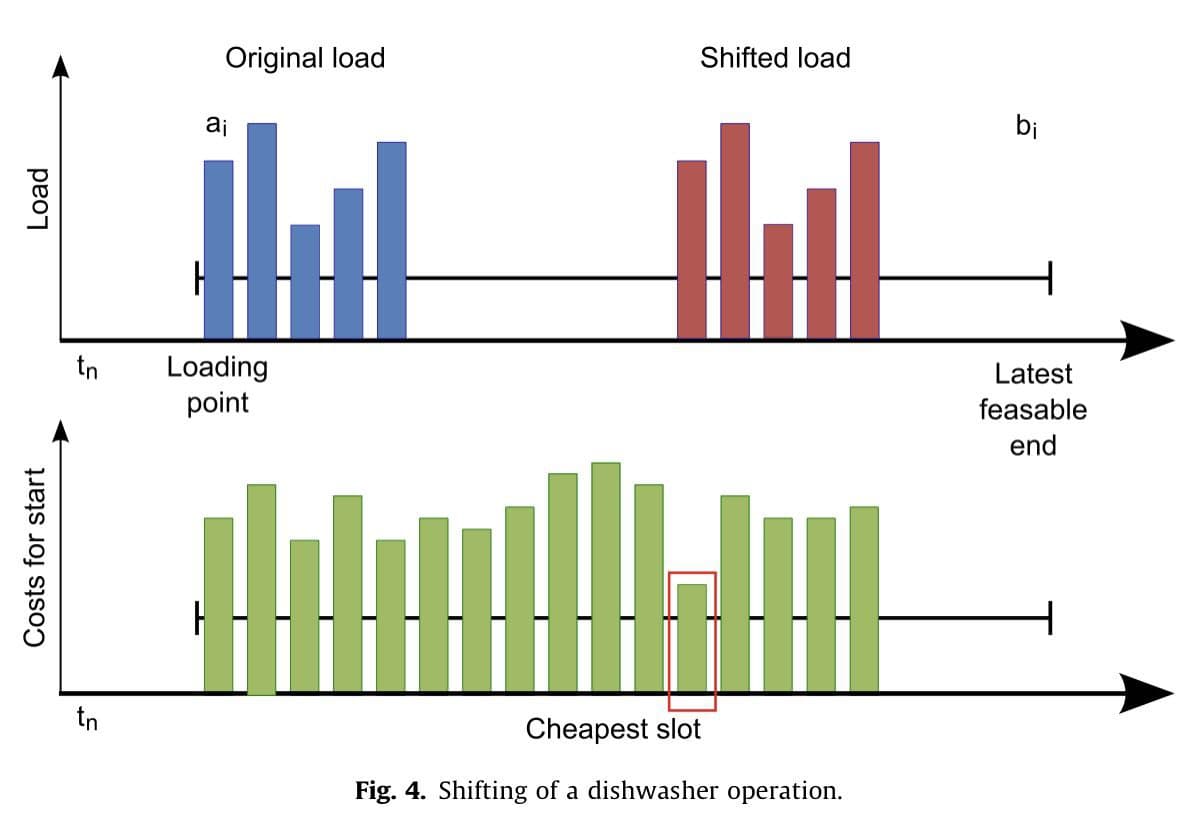

我知道如何使用pyomo来解决一个简单的多周期优化问题。如果目标函数中的和的边界是固定的,我可以写“和(…对于m.t中的t)”。要更好地理解我的意思,请参见以下代码示例:
from pyomo.environ import *
model = ConcreteModel()
model.T = RangeSet(5)
...
model.y = Var(model.T, domain=Binary)
model.i_pos = Var(model.T, domain=NonNegativeReals)
model.i_neg = Var(model.T, domain=NegativeReals)
...
c = 30 # setup cost: fixe Kosten pro Zeitschritt wenn in diesem Zeitschritt produziert werden muss
h_pos = 0.7 # cost per unit of holding inventory
h_neg = 1.2 # shortage cost per unit
P = 5.0 # maximum production amount per time step
...
def obj_rule(m):
return sum(c*m.y[t] + h_pos*m.i_pos[t] + h_neg*m.i_neg[t] for t in m.T)
model.obj = Objective(rule=obj_rule, sense=minimize)
现在,我所提到的能量优化问题的问题是,我不知道如何在pyomo的和的边界中包含一个变量。在这种情况下,变量s_n,i(参见链接:问题描述)描述了洗碗机的开始时间段,但也包括在我的目标函数的总和中,该目标函数使成本最小化。所以我需要把变量s_n,放入目标函数的“for t in m.t”部分。
我从论文中略微修改了这个问题:
这是我当前的代码:
from pyomo.environ import *
model = ConcreteModel()
# 7 time steps
model.T = RangeSet(7)
a = 1 # earliest starting time slot for the dishwasher
b = 7 # lastest ending time slot for the dishwasher
d = 2 # duration dishwasher in h
p = 1 # power dishwasher in kW
# electricity cost per time step in €/kWh
cost = {1: 0.4, 2: 0.3, 3: 0.3, 4: 0.15, 5: 0.25, 6: 0.30, 7: 0.35}
# definition of the variable s_n,i
model.start = Var(bounds=(a, b-d), domain=NonNegativeReals)
def obj_rule(m):
return sum(cost[t]*p for t in m.T)
model.obj = Objective(rule=obj_rule, sense=minimize)
solver = SolverFactory('glpk')
solver.solve(model)
谢谢你的帮助!
欢迎来到网站。你的问题更像是数学编程,而不是编码问题,但是让我们试一试...
我希望您对整数规划有一定的了解,因为这就是您需要解决此问题的地方,以修复挂起的部分。
考虑更改start变量。(为了方便起见,我们将其重命名为Y)让我们确定Y_j是一个二进制变量,表示在j期间启动机器的决定,其中j是允许启动的期间T的子集。现在我们在你的目标函数中有一些东西要处理。。。。
然后,在目标中,我们将查看求和元素,并查看在当前或前2个时间段(假设机器运行3个时间步)中Y_j是否为1(已选择)。
或者,您可以引入另一个变量来指示机器是否在任何特定时期运行,并根据Y_j设置约束来强制该变量。
您将需要一个或两个约束Y_j取决于您如何设置问题,当然,值得注意的是,sum(Y_j)=1
如果你卡住了,请回复。
编辑:执行如下
对此有几种方法。下面的一个使用2个变量作为开始期,一个用于“运行”。我认为你可以用一个更复杂的目标函数来巧妙地处理它,只需使用“开始”变量,但这是按照你的评论来的。
# pick the cheapest 2-consecutive periods to run an appliance
import pyomo.environ as pyo
# Data
costs = { 1:10,
2:5,
3:7,
4:15}
num_periods = 4
run_time = 2 # the number of periods the machine runs
m = pyo.ConcreteModel('appliance runner')
# SETS
m.T = pyo.RangeSet(num_periods)
m.T_start = pyo.RangeSet(num_periods - (run_time - 1)) # legal starts {1,2,3}
# VARS
m.Y = pyo.Var(m.T_start, domain=pyo.Binary) # the period to START
m.X = pyo.Var(m.T, domain=pyo.Binary) # machine running
# CONSTRAINTS
# must start at least once
m.C1 = pyo.Constraint(expr=sum(m.Y[t] for t in m.T_start) >=1 )
# periods after the start, the machine must be on for run_time
# (this is the tricky one... couple ways to do this...)
def running(self, t):
return m.X[t] >= sum(m.Y[t2] for t2 in
range(t, t-run_time, -1)
if t2 in m.T_start)
m.C2 = pyo.Constraint(m.T, rule=running)
# m.pprint() <-- use this to see what was created in this constraint
# OBJ
m.OBJ = pyo.Objective(expr=sum(m.X[t]*costs[t] for t in m.T))
solver = pyo.SolverFactory('glpk')
results = solver.solve(m)
print(results)
m.display()