用Python计算直线和圆的切圆公式

提问者：小点点

用Python计算直线和圆的切圆公式

我有线和圆模型（我知道用数据形成的方程）。我想找到与我的线和圆相切的切点或黄色圆方程（半径由我决定）。

一开始我试图分别解决相互方程线和黄色圆圈和圆和黄色圆圈减少到3方程到2方程，但我找不到一个解决方案可能计算错误。

通过python找到这些点有没有更明确的方法或意见？

例如：

圆-1：（x-8,98）^2（y-42,53）^2=6,4^2

第1行：y=22,904x-115,9707

切圆：（x-a）^2（y-b）^2=14^2

切点（在AutoCAD中创建）：

X1=6,2028 Y1=26,0978

X2=12,4953 Y2=37,1832

共1个答案

匿名用户

您的问题有多种解决方案。

你有6个未知数，所以解决问题的最简单方法（不一定是最快的）是使用定义的约束制作6个方程。之后，您可以使用像Sympy这样的符号数学引擎来求解方程组。

让我们从定义方程开始。

我们知道P1和第二个圆的中心（其中心以下记为（x_a2，ya_2））之间的线-2垂直于斜率等于a的线1。因此垂直线-2的斜率等于-1/a。由于A2和P1在线-2上，我们有以下

P1在圆圈-2上，所以

P1在第1行，所以

我们知道两个圆心之间的欧几里得距离等于r1 r2，所以

P2在圆圈-1上，

P2在圆圈-2上，

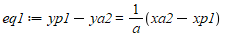
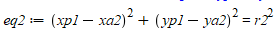
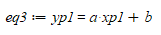
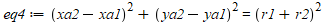
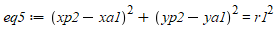
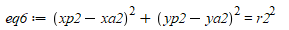
我们终于有了6个方程，所以我们可以用Sympy来求解方程组。

我建议在Jupyter笔记本上运行以下代码

#%%
#imports

import sympy as sp
from sympy import Eq
from sympy.physics.mechanics import dynamicsymbols
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)

#%%
#Unknows and variables definition 

x_a1, y_a1, r_1, r_2, a, b = 8.98, 42.53, 6.4, 14, 22.904, -115.97

x_a2, y_a2, x_p1, y_p1, x_p2, y_p2 = dynamicsymbols('x_a2 y_a2 x_p1 y_p1 x_p2 y_p2')

#%%
#equations definition

eq1 = Eq(y_p1-y_a2,(1/a)*(x_a2-x_p1))

eq2 = Eq((x_p1-x_a2)**2+(y_p1-y_a2)**2,r_2**2)

eq3 = Eq(y_p1, a * x_p1 + b)

eq4 = Eq((x_a2-x_a1)**2+(y_a2-y_a1)**2,(r_1 + r_2)**2)

eq5 = Eq((x_p2-x_a1)**2+(y_p2-y_a1)**2,r_1**2)

eq6 = Eq((x_p2-x_a2)**2+(y_p2-y_a2)**2,r_2**2)

eq4 = sp.expand(eq4)

eq5 = sp.expand(eq5)

#%%
#solve the system

sp.solve((eq1,eq2,eq3,eq4,eq5,eq6), (x_a2, y_a2, x_p1, y_p1, x_p2, y_p2))

以下是我得到的解决方案（按顺序排列：[x_a2y_a2x_p1y_p1x_p2y_p2]），

[(−7.61137900888098, 30.6604531432888, 6.37529636566885, 30.0497879592794, 3.77486148740989, 38.8062205939729), (−6.51375646949495, 55.8003997853864, 7.47291890505488, 55.1897346013771, 4.11921365662903, 46.6932626777683), (20.1893606892033, 25.4856392628135, 6.20268531465346, 26.0963044468229, 12.496662177005, 37.1827495726474), (21.6322053306201, 58.5325529298243, 7.64552995607028, 59.1432181138336, 12.9493193194102, 47.5504087622978)]

第三个解决方案是AutoCAD给出的解决方案（以及您图中所示的解决方案）