我要求解其中是一个非常大的平方正定对称分块矩阵，和是向量。当我说大时，我指的是矩阵的大到。

这里有一个例子，是我想要求解的一个小得多但有代表性的矩阵。

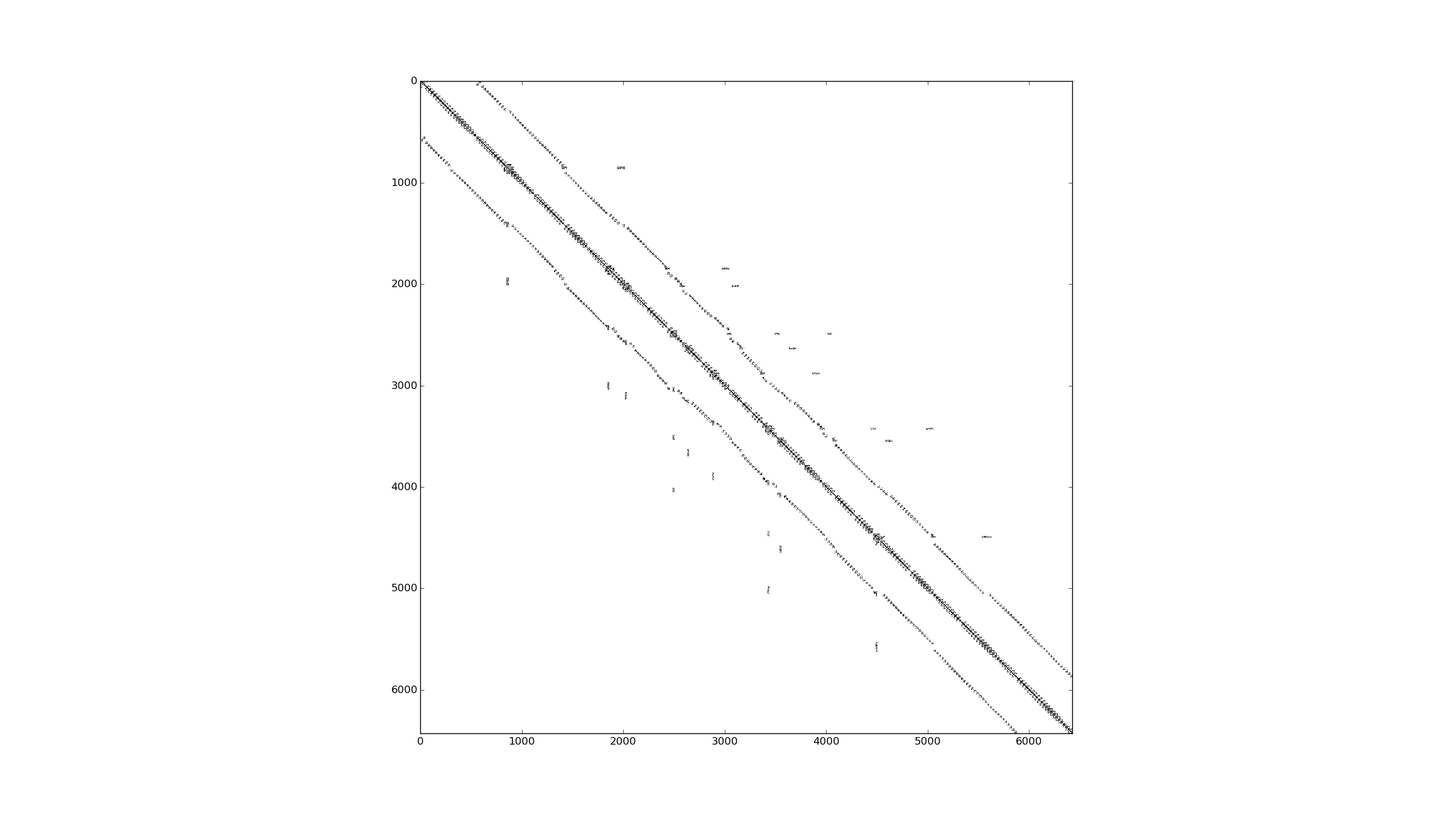
这里是相同的矩阵放大，显示它是由密集矩阵块组成的。

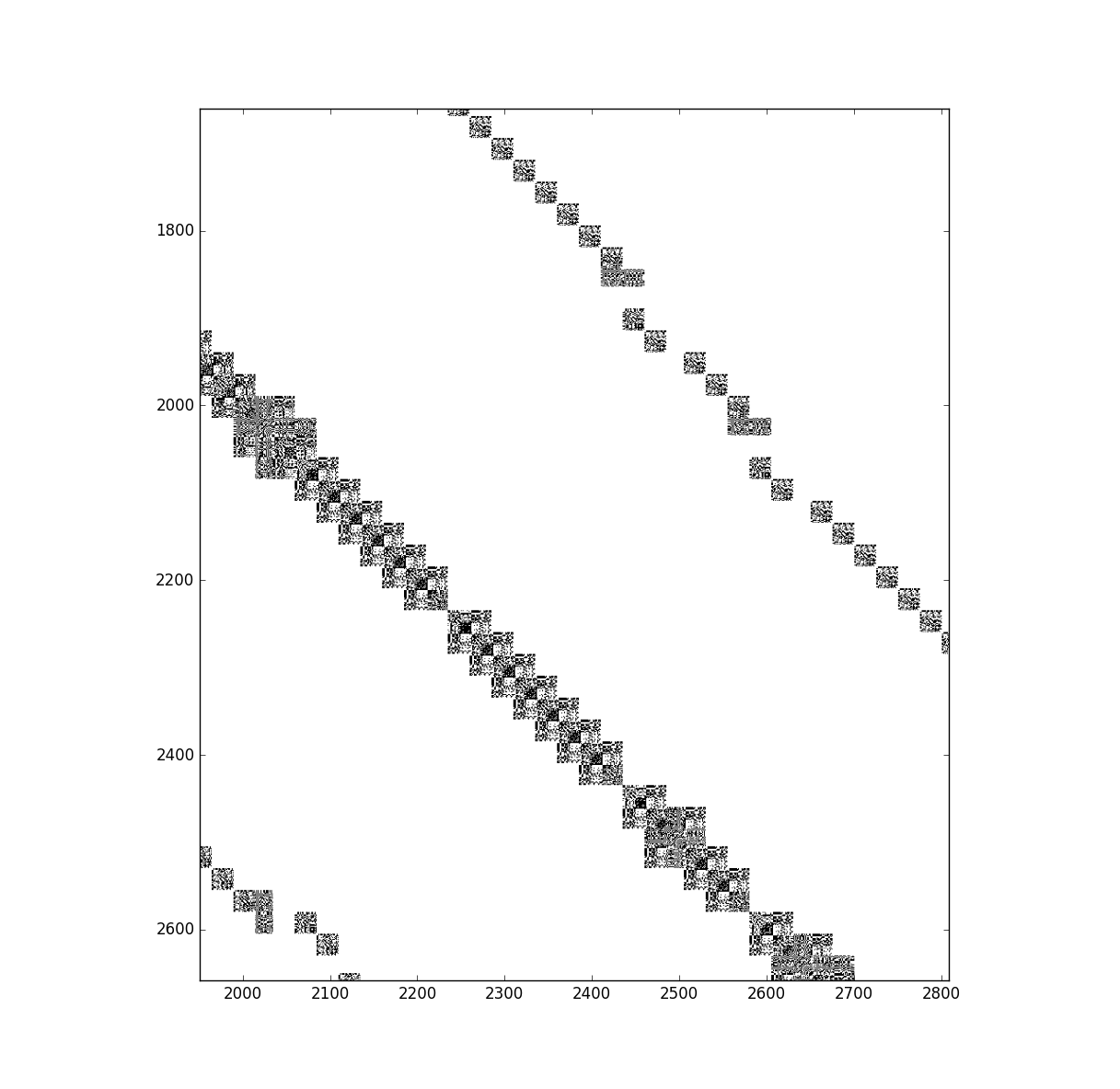
我以前使用过Eigen's Cholesky solver（参见此处，此处和更远的此处），它在下工作良好，但在下，Cholesky solver太慢了。然而，我没有利用我有一个块矩阵的事实。显然，存在求解稀疏分块矩阵的算法（如分块cholesky分解）。

我特别想知道Eigen是否有优化算法，使用因式分解或迭代方法，对于稀疏稠密的块矩阵，我可以使用？

你也可以建议其他算法，可能是理想的解决我的矩阵？我的意思是，据我所知，至少对于因式分解来说，寻找置换矩阵是NP困难的，因此存在许多不同的启发式方法，据我所知，人们对不同的矩阵结构（例如带状矩阵）建立了一种直觉，以及哪种算法对它们最有效。我还没有这种直觉。

我目前正在研究使用共轭梯度法。我自己用C++实现了这一点，但仍然没有利用矩阵是块矩阵这一事实。

//solve A*rk = xk
//Eigen::SparseMatrix<double> A;
//Eigen::VectorXd rk(n);
Eigen::VectorXd pk = rk;

double rsold = rk.dot(rk);
int maxiter = rk.size();
for (int k = 0; k < maxiter; k++) {
    Eigen::VectorXd Ap = A*pk;  
    double ak = rsold /pk.dot(Ap);
    xk += ak*pk, rk += -ak*Ap;      
    double rsnew = rk.dot(rk);
    double xlength = sqrt(xk.dot(xk));
    //relaxing tolerance when x is large
    if (sqrt(rsnew) < std::max(std::min(tolerance * 10000, tolerance * 10 * xlength), tolerance)) {
        rsold = rsnew;
        break;
    }
    double bk = rsnew / rsold;
    pk *= bk;
    pk += rk;
    rsold = rsnew;
}