

我有关于对称正定(SPD)矩阵的cholrank1更新程序(维基百科)。
function [L] = cholupdate(L,x)
p = length(x);
for k=1:p
r = sqrt(L(k,k)^2 + x(k)^2);
c = r / L(k, k);
s = x(k) / L(k, k);
L(k, k) = r;
L(k+1:p,k) = (L(k+1:p,k) + s*x(k+1:p)) / c;
x(k+1:p) = c*x(k+1:p) - s*L(k+1:p,k);
end
end
它与LL分解一起工作。我尝试像下面这样修复过程,以便与LDL分解一起工作(即不调用sqrt):
function [L] = cholupdate_ldl(L,x)
p = length(x);
for k=1:p
r = L(k,k) + x(k)^2;
c = r / L(k, k);
s = x(k) / L(k, k);
L(k, k) = r;
L(k+1:p,k) = (L(k+1:p,k) + s*x(k+1:p)) / c;
x(k+1:p) = sqrt(c)*(x(k+1:p) - x(k)*L(k+1:p,k));
end
end
它运行良好,但我被迫使用SQRT。我怎样才能在完全不使用sqrt的情况下更新LDL分解呢?
有很多种方法。参见Gill,Golub,Murray和Saunders(1974):《计算数学中修正矩阵分解的方法》。为了正式地总结你的问题,我引用文件中的内容:
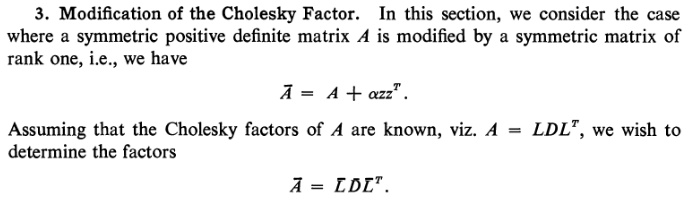
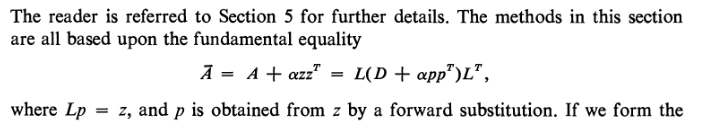
最后我们讨论算法:
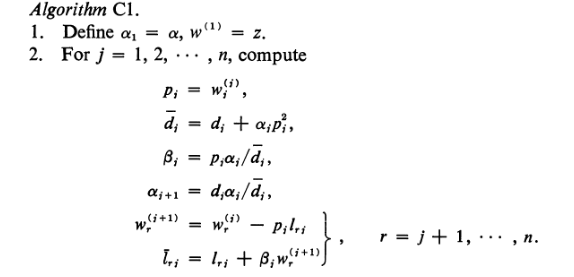
下面是我在MATLAB中的实现:
function [L1,D1] = ldlt_update(L0,D0,z)
n = size(L0,1) ;
D1 = zeros(n,n) ;
L1 = zeros(n,n) ;
a = 1 ;
w = z ;
for jj = 1:n
p = w(jj) ;
D1(jj,jj) = D0(jj,jj) + a*p^2 ;
b = p*a/D1(jj,jj) ;
a = D0(jj,jj)*a/D1(jj,jj) ;
for r = jj+1:n
w(r) = w(r) - p*L0(r,jj) ;
L1(r,jj) = L0(r,jj) + b*w(r) ;
end
end
end
在上面引用的论文和Gill,Murray和Wright(1982):《实用最优化》中有一种替代算法。Brian Borchers有一套完整的MATLAB代码,用于处理实对称正定LDLT分解,如Golub和Van Loan(2013):Matrix Computations和他的网站上所定义的那样。