

我最近偶然发现了2048这个游戏。您可以通过在四个方向中的任何一个方向移动相似的平铺来合并它们,从而生成“更大”的平铺。每次移动后,在随机空位置出现一个新的平铺,其值为2或4。当所有方框都填满并且没有可以合并平铺的招式,或者您创建了一个值为2048的平铺时,游戏终止。
第一,我需要遵循一个明确的战略来达到目标。所以,我想到为它写一个程序。
我当前的算法:
while (!game_over) {
for each possible move:
count_no_of_merges_for_2-tiles and 4-tiles
choose the move with a large number of merges
}
我正在做的是,在任何一点上,我都会尝试合并值为2和4的瓦片,也就是说,我尝试有2和4瓦片,尽可能少。如果我试着这样做,所有其他的瓷砖会自动被合并,这个策略看起来很好。
但是,当我实际使用这个算法时,在游戏结束前我只能得到大约4000分。AFAIK的最高积分是略高于20000分,这比我现在的分数要大得多。有没有比上述更好的算法呢?
我开发了一个使用expectimax优化的2048 AI,而不是@Ovolve算法使用的minimax搜索。AI简单地对所有可能的移动执行最大化,然后是对所有可能的瓦片产生的期望(由瓦片的概率加权,即,对于4,10%,对于2,90%)。据我所知,不可能修剪ExpectMax优化(除了删除极不可能的分支),因此使用的算法是经过仔细优化的蛮力搜索。
AI在其默认配置(最大搜索深度为8)下执行移动需要10ms到200ms的时间,这取决于棋盘位置的复杂性。在测试中,人工智能在整个游戏过程中实现了每秒5-10步的平均移动速率。如果搜索深度被限制在6步以内,那么AI可以轻松地每秒执行20+步,这使得观看变得很有趣。
为了评估AI的分数表现,我运行了AI 100次(通过远程控制连接到浏览器游戏)。对于每个平铺,以下是该平铺至少获得一次的游戏比例:
2048: 100%
4096: 100%
8192: 100%
16384: 94%
32768: 36%
所有跑的最小得分为124024分;取得的最高分是794076分。中位数得分为387222。人工智能从未失败过获得2048分牌(因此它从未在100场比赛中输掉比赛哪怕一次);事实上,它在每次运行中至少实现了一次8192瓦片!
下面是最佳跑路的截图:

这款游戏在96分钟内走了27830步,平均每秒走4.8步。
我的方法将整个板(16个条目)编码为单个64位整数(其中块是nybble,即4位块)。在64位机器上,这使得整个电路板可以在单个机器寄存器中传递。
位移位操作用于提取单个行和列。单行或列是一个16位的量,因此大小为65536的表可以对在单行或列上操作的转换进行编码。例如,移动被实现为对预先计算的“移动效果表”的4次查找,该“移动效果表”描述每次移动如何影响单个行或列(例如,“向右移动”表包含条目“1122->0023”,该条目描述当向右移动时行[2,2,4,4]如何变成行[0,0,4,8])。
评分也是使用表查找完成的。这些表包含在所有可能的行/列上计算的启发式得分,板的结果得分只是每行和每列的表值之和。
这种棋盘表示法,以及用于移动和评分的表查找方法,允许人工智能在短时间内搜索大量的游戏状态(在我2011年年中笔记本电脑的一个核心上,每秒超过1000万个游戏状态)。
expectimax搜索本身被编码为递归搜索,该递归搜索在“期望”步骤(测试所有可能的瓦片产卵位置和值,并根据每个可能性的概率加权其优化得分)和“最大化”步骤(测试所有可能的移动并选择具有最佳得分的移动)之间交替进行。当它看到先前看到的位置(使用换位表),当它达到预定义的深度限制,或者当它达到极不可能的板状态(例如,通过从起始位置获得一行中的6个“4”块来达到)时,树搜索终止。典型的搜索深度是4-8次移动。
使用了几种启发式来指导优化算法朝着有利的位置进行。启发式算法的正确选择对算法的性能有很大的影响。各种启发式算法被加权并组合成一个位置得分,该得分决定了给定董事会位置的“好”程度。然后,优化搜索将以所有可能的董事会位置的平均得分最大化为目标。实际得分,如游戏所示,并不用于计算棋盘得分,因为它的权重太重,有利于合并瓷砖(当延迟合并可能产生很大的好处时)。
最初,我使用了两个非常简单的启发式,为开放的方块和在边缘具有大值的方块授予“奖金”。这些启发式算法表现得很好,经常达到16384,但从未达到32768。
PetrMorávek(@xificurk)接受了我的人工智能,并添加了两个新的启发式。第一个启发式是惩罚非单调的行和列,这些行和列随着秩的增加而增加,确保小数字的非单调行不会强烈地影响分数,但大数字的非单调行却会严重地伤害分数。第二种启发式计算了除了开放空间之外的潜在合并(相邻相等值)的数量。这两种启发式方法将算法推向单调的棋盘(更容易合并)和具有大量合并的棋盘位置(鼓励算法在可能的情况下对齐合并以获得更大的效果)。
此外,Petr还使用“元优化”策略(使用称为CMA-ES的算法)优化了启发式权重,其中权重本身被调整以获得可能的最高平均得分。
这些变化的影响是极其显著的。该算法从大约13%的时间实现16384块到超过90%的时间实现它,并且该算法开始在超过1/3的时间实现32768块(而旧的启发式从来没有产生过32768块)。
我相信启发式还有改进的余地。这个算法肯定还不是“最优”的,但我觉得它已经很接近了。
人工智能在超过三分之一的游戏中达到了32768分,这是一个巨大的里程碑;如果有人类玩家在官方游戏中获得了32768的成绩,我会感到惊讶的(例如,没有使用像savestates或undo这样的工具)。我想65536瓷砖触手可及!
你可以自己试试人工智能。代码可在https://github.com/nneonneo/2048-ai上获得。
我是其他人在本文中提到的人工智能程序的作者。您可以查看AI的实际操作或阅读源代码。
目前,在我笔记本电脑的浏览器中运行javascript程序可以达到90%的胜率,每次移动大约需要100毫秒的思考时间,所以虽然还不完美(还不完美!)它表现得很好。
由于该游戏是一个离散状态空间,完美信息,回合制游戏,就像国际象棋和跳棋,我使用了同样的方法,已经被证明在这些游戏上工作,即minimax搜索与alpha-beta剪枝。由于已经有很多关于该算法的信息,我将只讨论我在静态求值函数中使用的两种主要的启发式,它们形式化了其他人在这里表达的许多直觉。
这种启发式方法试图确保瓦片的值沿左/右和上/下方向都在增加或减少。这一启发式方法本身就抓住了许多其他人提到的直觉,即价值较高的瓷砖应该聚集在一个角落里。它通常会防止价值较小的瓷砖被孤立,并将使董事会非常有条理,较小的瓷砖级联并填充到较大的瓷砖中。
这是一个完美单调网格的截图。我通过运行算法,并设置eval函数来忽略其他启发式,只考虑单调性来获得这一点。

仅上述启发式倾向于创建其中相邻瓦片的值在减少的结构,但当然为了合并,相邻瓦片需要是相同的值。因此,平滑度启发式只是测量相邻瓷砖之间的值差异,试图最小化这个计数。
Hacker News上的一位评论者用图论的方法对这个想法进行了一个有趣的形式化。
这是一个完美光滑的网格的截图,这是这个极好的模仿叉的功劳。

最后,有一个惩罚,因为有太少的免费瓷砖,因为选项可能会很快耗尽当游戏板变得太局促。
就这样!在优化这些标准的同时搜索游戏空间会产生非常好的性能。使用像这样的通用方法而不是显式编码的移动策略的一个优点是,算法经常可以找到有趣的和意想不到的解决方案。如果你看着它奔跑,它经常会做出令人惊讶但又有效的动作,比如突然切换它正在建造的墙壁或角落。
这里演示了这种方法的威力。我取消了瓷砖值的上限(所以它在达到2048年后一直保持),下面是经过八次测试后的最佳结果。

是的,那是4096和2048。=)这意味着它在同一块棋盘上三次实现了难以捉摸的2048块。
我开始对这个游戏的人工智能的想法感兴趣,它不包含硬编码的智能(即没有启发式,评分函数等)。人工智能应该只“知道”游戏规则,并“弄清楚”游戏玩法。这与大多数AIs(如本文中的AIs)形成了对比,在这些AIs中,游戏玩法本质上是由一个代表人类对游戏理解的评分函数控制的蛮力游戏。
我发现了一个简单却出奇的好玩算法:为了确定给定棋盘的下一步棋,人工智能在内存中使用随机棋玩游戏,直到游戏结束。这样做了几次,同时保持跟踪结束游戏的分数。然后计算每个起始动作的平均结束分数。最后平均得分最高的起始动作被选为下一个动作。
每一步只要跑100次(即在记忆游戏中),人工智能就能达到2048块的80%的次数和4096块的50%的次数。使用10000次运行,2048块得到100%,4096块得到70%,8192块得到约1%。
在行动中看到它
最佳得分如下所示:
关于这个算法的一个有趣的事实是,尽管随机游戏并不令人惊讶地非常糟糕,但选择最好的(或最不坏的)移动会导致非常好的游戏:一个典型的人工智能游戏可以达到70000点并持续3000次移动,然而内存中任意位置的随机游戏在死亡之前在大约40次额外移动中平均产生340个额外的点数。(您可以通过运行AI并打开调试控制台来查看这一点。)
这张曲线图说明了这一点:蓝线显示了每一步棋后的棋盘得分。红线显示该算法从该位置获得的最佳随机运行结束游戏得分。本质上,红色值是“拉”蓝色值向上,因为它们是算法的最佳猜测。很有趣的是,在每一点上,红线都比蓝线高出一点点,而蓝线却在继续增加。
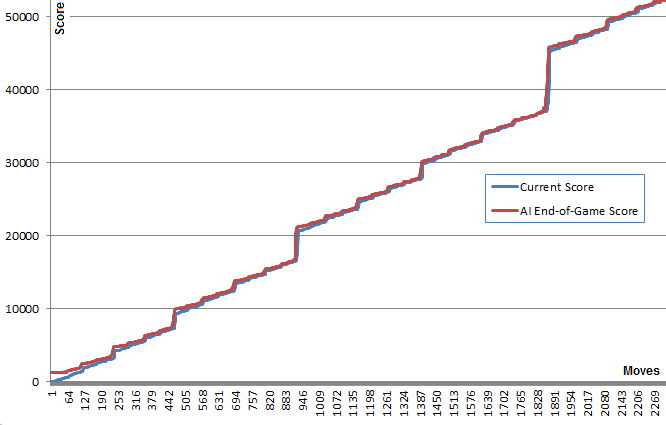
我发现这是相当令人惊讶的,算法并不需要实际预见好的游戏玩法,以选择产生它的移动。
后来搜索发现,该算法可能属于纯蒙特卡罗树搜索算法。
首先,我创建了一个JavaScript版本,在这里可以看到它的实际操作。这个版本可以在相当的时间内运行100次。打开控制台以获取更多信息。(来源)
后来,为了玩得更多,我使用了高度优化的@nneonneo基础设施,并用C++实现了我的版本。这个版本允许高达100000运行每一步,甚至1000000,如果你有耐心。提供建筑说明。它运行在控制台,也有一个远程控制播放网页版本。(来源)
令人惊讶的是,增加跑动次数并没有大幅提升游戏玩法。在4096和所有较小的点位的80000点附近,这个策略似乎有一个极限,非常接近于达到8192点的点位。将跑步次数从100次增加到100000次会增加达到这个分数限制(从5%增加到40%)但不突破它的几率。
跑10000次,在关键位置附近临时增加到1000000次,成功打破这一障碍的次数不到1%,达到了129892和8192的最高分数。
在实现这个算法之后,我尝试了许多改进,包括使用最小或最大分数,或最小,最大和平均的组合。我还尝试使用深度:不是尝试每步走K步,而是尝试了给定长度的每步走K步(例如“向上,向上,向左”),并选择最佳得分移动列表的第一步。
后来我实现了一个计分树,它考虑了在给定的移动列表之后能够打出一个移动的条件概率。
然而,与简单的第一个想法相比,这些想法都没有显示出任何真正的优势。我把这些想法的代码注释掉在C++代码中。
我确实添加了一个“深度搜索”机制,当任何一个运行设法意外地到达下一个最高平铺时,它将运行次数临时增加到1000000。这提供了时间上的改进。
我很想知道是否有人有其他的改进想法来保持AI的领域独立性。
只是为了好玩,我还将AI实现为一个书签,与游戏的控制挂钩。这使得人工智能可以与原始游戏和它的许多变体一起工作。
由于AI的领域无关性,这是可能的。有些变体是非常独特的,如六角形克隆。