针对多个对手的minimax算法的扩展

提问者：小点点

针对多个对手的minimax算法的扩展

minimax算法对于两个玩家来说都是很好的描述，比如tic-tac-toe。我需要为坦克游戏写一个AI。在这个游戏中，坦克必须在有障碍物的迷宫中移动。目的是收集硬币堆。如果只有两个参与者，则可以实现极小极大算法。但是如何在两个以上的时间内实现它呢？在每个回合中，每个球员都会尽力最大化自己的获胜优势。我不能认为所有的玩家都是一个敌人，他们只想减少我的获胜优势，就像最初的minimax算法那样创建两个玩家级别。如果问题格式不好，请原谅。对这个论坛来说还是新鲜事

共3个答案

匿名用户

Mihai Maruseac说MiniMax不能再使用了，这只是部分正确。如果“MiniMax”指的是MiniMax的“标准变体”，那么他完全正确！（这就是他的意思。）然而，你也可以把MiniMax看作MaxiMax，两个玩家各自最大化自己的奖励（这正是AlphaWolf在问题中所写的）。因此，对n个参和者的推广被称为Max^n，这在某种程度上仍然可以被视为极小极大。无论如何，下面我将解释为什么标准的2人极小极大不能用于3人或更多人的多人游戏环境。然后，最后，我给出了正确的替代方案，即Max^n算法。

因此，让我们先考虑一下，是否可以简单地将2人MIMPAX转换成N玩家MIMPAX，将所有对手视为最小玩家，也就是说，他们都会尽量减少Max玩家的奖励。

好吧，你不能！让我解释一下原因。

首先，回想一下，MiniMax总是专门考虑两人零和博弈。因此，MiniMax通常只描述一个游戏结果。然而，从技术上讲，有两个！最大玩家和最小玩家的游戏。因此，为了在形式上完全正确，我们必须为每个搜索节点提供一个2元组作为游戏结果，比如（payoff-P1，payoff-P2），其中payoff-P1是P1（MAX）的结果，payoff-P2是P2（MIN）的结果。然而，由于我们通常考虑零和游戏，我们知道它们的总和总是等于零，即PayOff-P1 PayOffelP2＝0。因此，我们总是可以推断出对方的胜利，因此只能从P1的角度来表示结果。此外，最小化收益-P2与最大化收益-P1相同。

对于几乎所有的游戏（除了在现实生活中，当心理因素起作用时，说报复而不关心自己的损失），我们总是假设所有的代理都玩理性的。当我们谈论两个以上的球员时，这将是非常重要的！什么是理性？每个玩家都以最大化自己的奖励为目标（！）再次假设所有其他玩家也玩理性。

回到2人零和：我们确实利用/假设了理性，因为P1（MAX）已经最大化了它的奖励（根据定义），而MIN也最大化了它自己的奖励，因为它最小化了MAX的奖励（这是因为零和与最大化MINs奖励）。因此，两个玩家都最大化了自己的奖励，因此玩得很理性。

现在让我们假设我们有2个以上的玩家，简单地说3个。

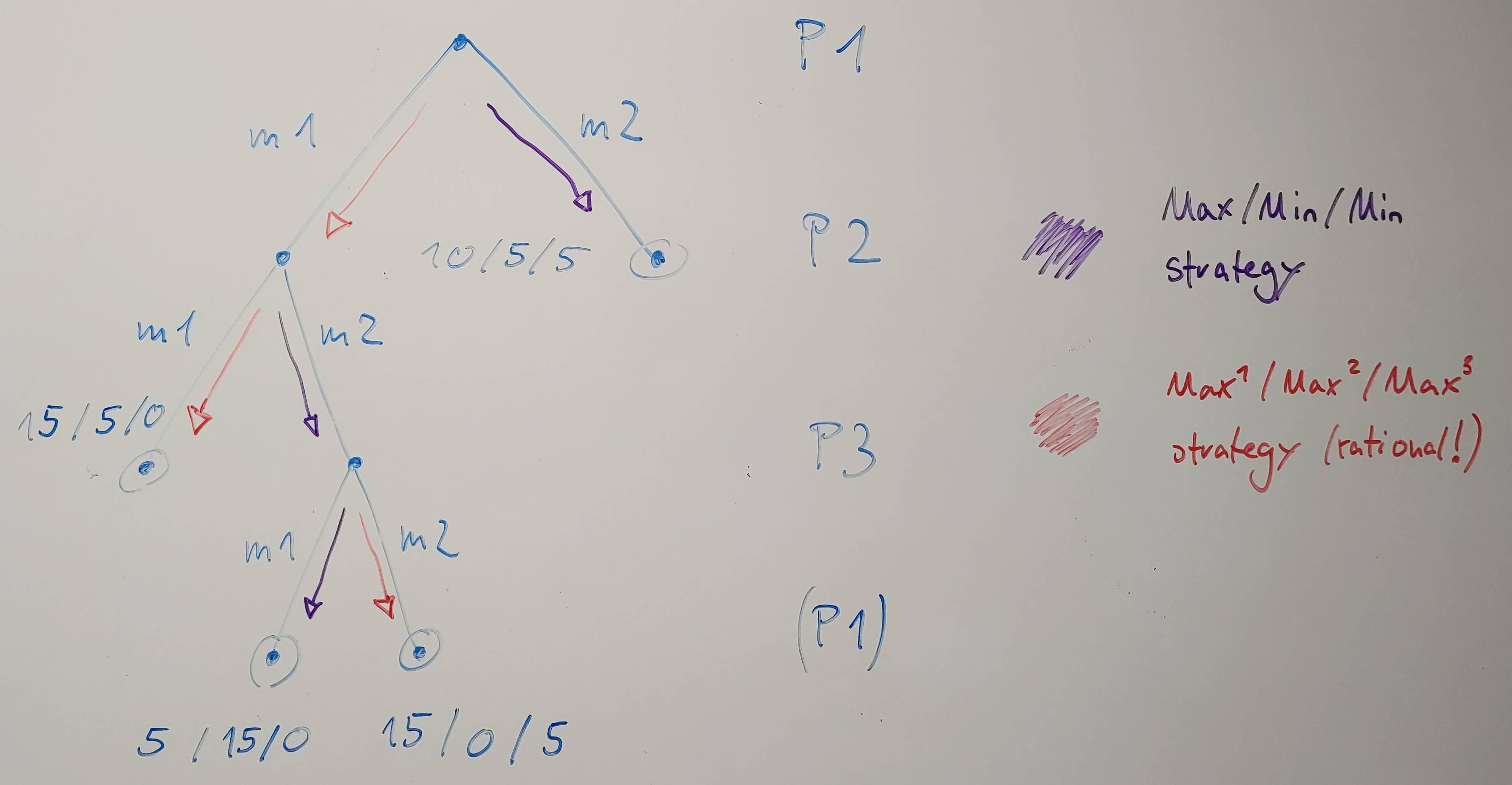
我们在这里看到的是：

像往常一样，我们有一个游戏树，三个玩家（P1，P2，P3）交替轮流。每个玩家有两个回合。最迟游戏在3次移动后结束（从技术上来说，P1必须转身，然后，但两个状态都是最终/叶子，所以游戏结束）。游戏描述了一个3人零和游戏（虽然零和不再需要了！所描述的一切也没有这个假设！）。
最大的胜利是20，分配给3个玩家。（请注意，在我的版本中，所有的胜利都是正面的。然而，它仍然是一个零和，因为所有的胜利总和都是完全相同的值，所以它可以很容易地转化为一个所有的胜利总和都是零。）获胜的结果显示为元组“收益-P1/收益-P2/收益-P3”。
此外，我用两种不同的颜色展示了各自玩家的钱包策略：紫色是假设只有P1是MAX玩家而其他玩家只最小化其奖励（而不关心自己的奖励）所追求的策略。红色显示了假设所有玩家都是MAX玩家的理性策略，即最大化他们自己的奖励。

那么，如果P2和P3被认为是MIN玩家，在这个游戏中会发生什么呢？他们会最小化P1的奖励，所以P1假设在玩m1时只得到5，因为P2可以通过玩m2来最小化P1的奖励。因此P1将选择其第二次移动m2获胜（仅）10。

然而，这两个对手都是MIN玩家的假设可以被视为两个玩家的合作（这是不合理的）。因为，当假设理性时，玩家P2永远不会玩m2，因为P3实际上会玩m3（所以P3赢得5而不是0）。但是假设所有对手最小化P1将使P2选择m2，因为这使P3能够打m1，从而将P1的胜利减少到5（而不是15，如果P3打得合理）。因此，使用MAX/MIN/MIN策略能够找到（或假设）对手合作对抗P1/MAX的策略，这在现实中（假设理性）永远不会发生！所以MiniMax适应2个以上的玩家显然是错误的。（也就是说，在发现永远不会发生的案件的意义上过于悲观。）我们可以在图中看到，当假设有理智能体时，P1应该打m1而不是m2，从而赢得15而不是只有10。

这表明极大极小值必须以不同的方式扩展。

如何显而易见：简单地用如上所述的向量分别表示每个玩家的结果。我们总是最大化当前玩家的结果，而不是根据轮到谁来最大化或最小化。因此，对于n个玩家，生成的算法也被称为Max^n。再次注意，MiniMax因此只是带有元组（payoff-P1，payoff-P2）的Max^2，其中payoff-P2被定义为-payoff-P1。

C.A.Luckhardt和K.B.Irani在《n人游戏的算法解决方案》中描述了Max^n算法，《第五届全国人工智能会议论文集》（AAAI'86），第158-162页，AAAI出版社。该文件可在以下网址公开获取：https://www.aaai.org/Papers/AAAI/1986/AAAI86-025.pdf

注意MiniMax，并且因此Max^n在实践中由于搜索空间的指数增加而从不使用，即，游戏树。相反，人们总是使用阿尔法/贝塔修剪，这是一个相当直观的扩展，永远不要访问/探索无论如何都没有意义的树分支。阿尔法/贝塔也被扩展到n玩家游戏

最后，让我添加一个非常有趣的观察结果：在两人零和极小极大中，计算的策略是“完美的”，因为它肯定会至少实现极小极大保证/计算的胜利。如果对手表现得不理性，即偏离其策略，那么结果只能更高。在n-游戏者零和极小极大中，也就是说，Max^n，情况不再是这样了！回想一下，P1的理性策略是玩m1，从而赢得15（如果对手玩理性）。然而，如果对手不理智，那么几乎一切都可能发生。在这里，如果P2不合理地玩m2，那么P1的输出完全取决于P3做什么，因此P1也可能赢得更少。原因是，在两人零和游戏中，对手的行为直接影响自己的结果——仅此而已！但是如果有3个或更多的玩家，胜利也可以分配给其他玩家。

匿名用户

您不能再为此使用minimax。除非你把一个人的利润最大化和另一个人的利润最小化作为一个混合目标。但这很难实现。

更好的方法是创建能够在战略层面上学习需要做什么的算法。将游戏转换成两个玩家的游戏：我对其他人，从这里开始。

匿名用户

使用多个最小化代理处理最小化函数的方法是运行一个最小化函数，所有代理的深度相同。一旦最小化代理全部完成，就可以在最后一个最小化代理上运行最大化函数。

# HOW YOU HANDLE THE MINIMIZING FUNCTION - If this pseudocode helps make better sense out of this.
scores = []
if agent == end_of_minimizing_agents: # last minimizing agent
    for actions in legal_actions: 
        depth_reduced = depth-1
        scores.append(max(successor_state, depth_reduced))
else:
    for actions in legal_actions: 
        scores.append(min(successor_state, depth))
bestScore = min(scores)
return bestScore