

我从2个月开始学习遗传算法。我知道最初的种群创造、选择、交叉和突变等过程。但不明白我们如何能够在每一代获得更好的结果,以及它与随机搜索最佳解决方案有何不同。下面我用一个例子来解释我的问题。
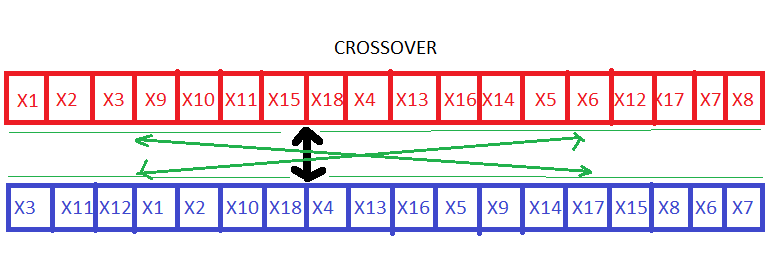
让我们以旅行推销员问题为例。假设我们有几个城市,如X1,X2。。。。我们必须找到最短的旅行路线。所以,当我们在选择最合适的人后进行交叉时,我们如何知道交叉后我们会得到更好的染色体。突变也是如此。
我觉得这只是一个城市的安排。计算旅行的最短距离。然后存储距离和排列。然后选择另一种安排/组合。如果比上一个排列好,则保存当前排列/组合和距离,否则放弃当前排列。通过这样做,我们将得到一些解决方案。
我只想知道随机选择和遗传算法的区别在哪里。在遗传算法中,是否有任何标准我们不能选择我们已经评估过的城市的布局/组合?
我不确定我的问题是否清楚。但我是开放的,我可以解释更多关于我的问题。如果我的问题不清楚,请告诉我。
随机算法每次都从一张完全空白的表格开始。每次迭代都会生成一个新的随机解,而不记得以前迭代中发生过什么。
遗传算法有历史,所以它不会从一张白纸开始,除非在最开始。每一代都选择解决方案种群中最好的,以某种方式突变,并推进到下一代。人口中最不优秀的成员被抛弃了。
遗传算法建立在以前成功的基础上,因此它们能够比随机算法进展得更快。一个非常简单的遗传算法的经典例子是黄鼠狼程序。它比随机机会更快地找到目标,因为每一代都从部分解开始,随着时间的推移,这些初始部分解更接近所需的解。
我认为你在问两件事。遗传算法有效的数学证明和经验证明,可以免除你的顾虑。
虽然我不知道是否有一般性的证明,但我很肯定约翰·霍兰德在他的著作《自然和人工系统中使用二进制编码的优化问题的适应》中至少给出了一个很好的证明草图。有一种叫做霍兰德的图式理论。但你知道,这是启发式的,所以从技术上讲,它不一定是。它基本上说,基因型提高平均适应度的短期方案在连续几代中呈指数形式出现。然后交叉将它们结合在一起。我认为这个证明只针对二进制编码,也受到了一些批评。
关于你的担忧。当然,你不能保证交叉会产生更好的结果。就像两个聪明或美丽的父母可能有丑陋愚蠢的孩子一样。遗传算法的前提是它不太可能发生。(据我所知)二进制编码的证据取决于这样一个理论,即一个好的部分模式将开始出现,并且考虑到基因型的长度应该足够长,居住在不同样本中的这些模式有机会合并成一个模式,以提高其整体适应性。
我认为从TSP的角度来看,这是相当容易理解的。交叉有助于将良好的子路径累积到一个样本中。当然,这一切都取决于交叉方法的选择。
此外,遗传算法通向解的路径也不是完全随机的。它通过随机机制朝某个方向移动,以逃避陷阱。如果你允许,你可能会失去最好的解决方案。它之所以有效,是因为它想朝着目前最好的解决方案发展,但你有大量的标本,它们分享着知识。它们都是相似的,但如果你保持多样性,可以将新的更好的部分模式引入到整个群体中,并纳入最佳解决方案中。这就是为什么人们认为人口多样性非常重要的原因。
最后,请记住,遗传算法是一个非常广泛的主题,您可以用几乎所有您想要的方式修改基础。你可以引入精英主义、禁忌、利基等。没有唯一的方法/实现。