

我的代码:
%% Example
x = 0:.01:4*pi;% x data
y = sin(x)+2;% y data
level = 2;% level
plot(x, y)
hold on
x_interest = 0:.01:x(length(y));
y_interest = sin(x_interest)+2;
xlim ([0 x(length(y))])
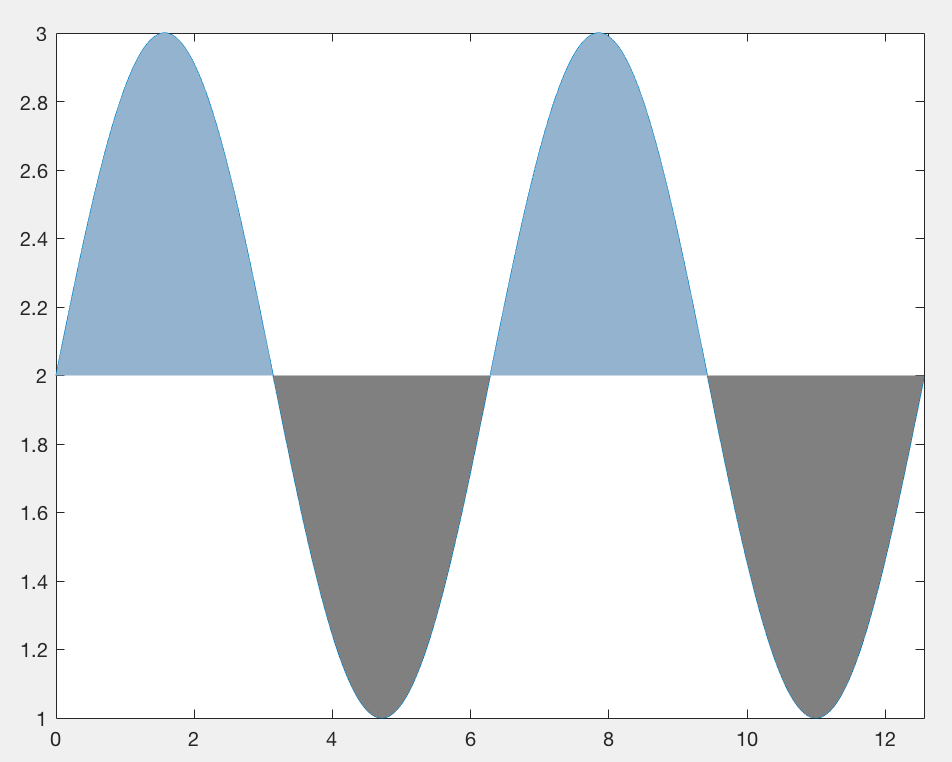
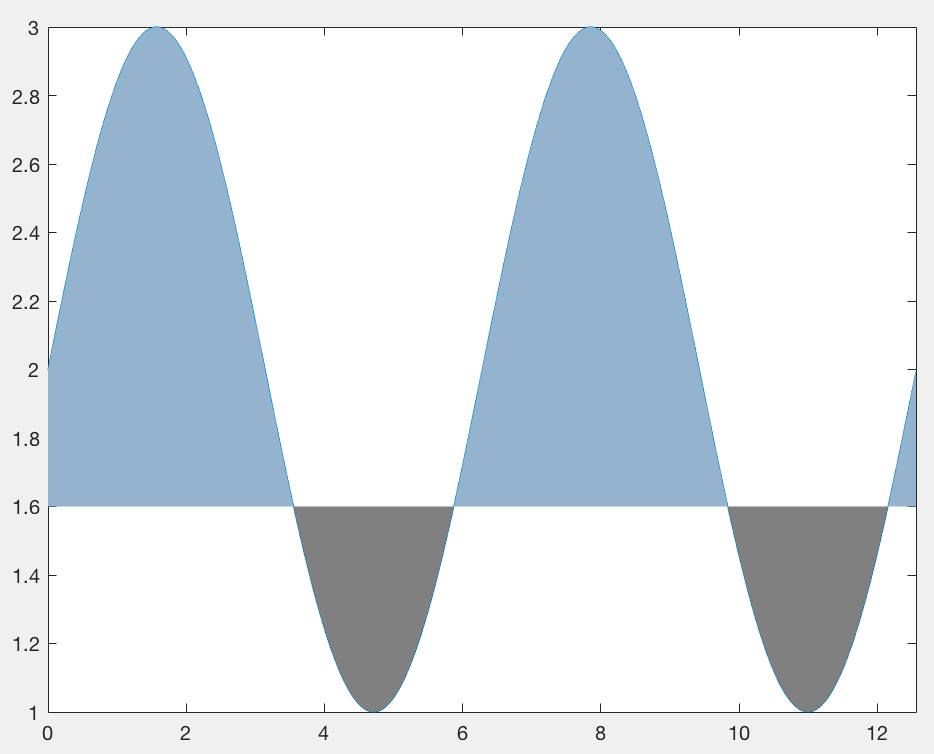
% Shaded area above level
area(x_interest, max(y_interest, level), level, ...
'EdgeColor', 'none', 'FaceColor', [.6 .7 .8], ...
'ShowBaseLine', 'off');
% Shaded area below level
area(x_interest, min(y_interest, level), level, ...
'EdgeColor', 'none', 'FaceColor', [.5 .5 .5], ...
'ShowBaseLine', 'off');
%%== This did not work ==%%
above = find(y_interest >= level);
below = find(y_interest <= level);
A_above = trapz(above)
A_below = trapz(below)
%% Integrate
plot(x, sin(x)+2)
fun = @(x) sin(x)+2;
integral(fun, 0, x(length(y)))
A = trapz(x,y)
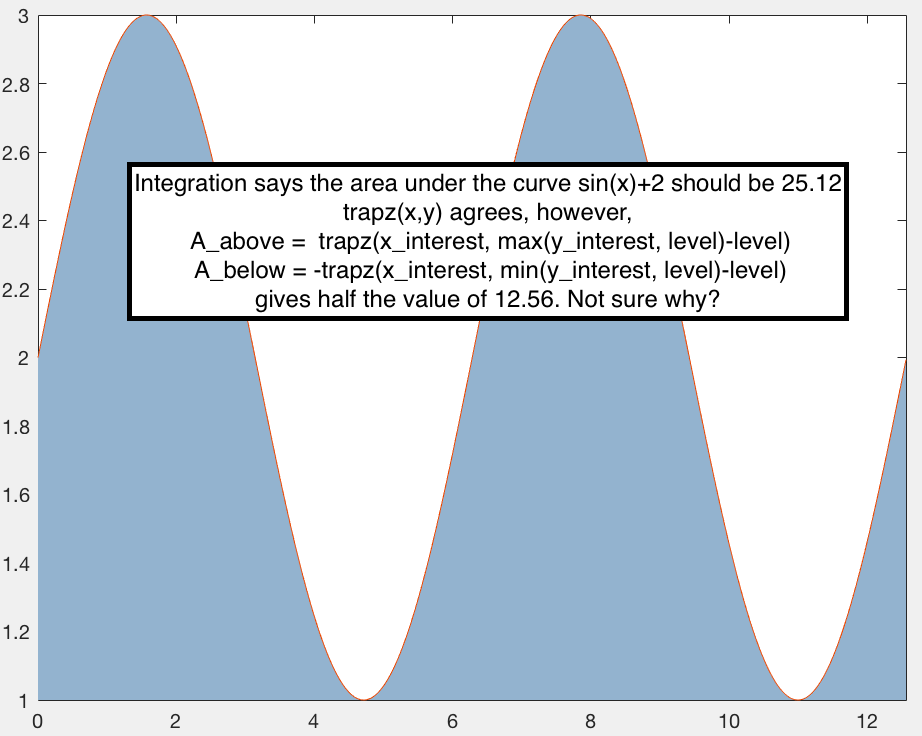
在一般意义上,函数trapz(x,y)(其中x和y是相同长度的向量)估计曲线下的面积f(x)=y。这个区域被函数f(x)和x轴夹在中间。
对于a_support,需要估计曲线之间的面积F1(x_interest)=max(y_interest,level)和F2(x_interest)=level。这与曲线F1(x_interest)下移级别下的区域相同。因此可以通过以下方法进行评估:
A_above = trapz(x_interest, max(y_interest, level)-level)
类似地,对于a_bellow:
A_below = -trapz(x_interest, min(y_interest, level)-level)