搜索二叉树节点的Java程序

1 简介

树是非线性数据结构，用于分层存储数据。树是称为节点的元素的集合。节点通过边连接并包含数据。树的第一个节点称为“根”。每个节点可能有也可能没有子节点。没有任何子节点的节点称为叶子。

二叉树是另一种树数据结构，其中每个节点最多可以有两个孩子。也就是说，二叉树中的每个节点都将具有数据，即左子节点和右子节点。

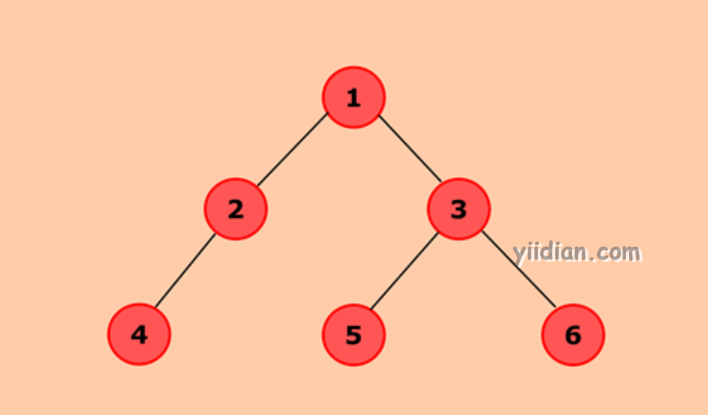
上图表示二叉树，其中1表示树的根节点。节点2的左子节点为4，节点3的左子节点为5，右子节点为6。节点4、5和6是叶节点，因为它们没有任何子节点。

2 算法思路

• 定义具有三个属性的Node类，即：左和右数据。在此，左代表节点的左子节点，右代表节点的右子节点。
• 创建节点时，数据将传递到该节点的data属性，并且左右都将设置为null。
• 定义另一个具有两个属性root和flag的类。
  • 根表示树的根节点，并将其初始化为null。
  • 该标志将用于检查树中是否存在给定的节点。最初，它将被设置为false。
• 它检查根是否为空，这意味着树为空。
• 如果树不为空，它将把温度数据与值进行比较。如果它们相等，则将标志设置为true并返回。
• 通过递归调用searchNode（）遍历左子树，并检查左子树中是否存在该值。
• 通过递归调用searchNode（）遍历右子树，并检查右子树中是否存在该值。

3 程序实现

/**
 * 一点教程网： http://www.yiidian.com
 */
public class SearchBinaryTree {  
  
      //Represent a node of binary tree  
      public static class Node{  
        int data;  
        Node left;  
        Node right;  
  
        public Node(int data){  
          //Assign data to the new node, set left and right children to null  
          this.data = data;  
          this.left = null;  
          this.right = null;  
        }  
      }  
  
      //Represent the root of binary tree  
      public Node root;  
  
      public static boolean flag = false;  
  
      public SearchBinaryTree(){  
        root = null;  
      }  
  
      //searchNode() will search for the particular node in the binary tree  
      public void searchNode(Node temp, int value){  
        //Check whether tree is empty  
        if(root == null){  
          System.out.println("Tree is empty");  
        }  
        else{  
          //If value is found in the given binary tree then, set the flag to true  
          if(temp.data == value){  
            flag = true;  
               return;  
          }  
          //Search in left subtree  
          if(flag == false && temp.left != null){  
             searchNode(temp.left, value);  
          }  
          //Search in right subtree  
          if(flag == false && temp.right != null){  
             searchNode(temp.right, value);  
          }  
        }  
      }  
  
      public static void main(String[] args) {  
  
        SearchBinaryTree bt = new SearchBinaryTree();  
        //Add nodes to the binary tree  
        bt.root = new Node(1);  
        bt.root.left = new Node(2);  
        bt.root.right = new Node(3);  
        bt.root.left.left = new Node(4);  
        bt.root.right.left = new Node(5);  
        bt.root.right.right = new Node(6);  
  
        //Search for node 5 in the binary tree  
           bt.searchNode(bt.root, 5);  
  
        if(flag)  
          System.out.println("Element is present in the binary tree");  
        else  
          System.out.println("Element is not present in the binary tree");  
      }  
    }  

输出结果为：

Element is present in the binary tree.