查找二叉树中最大距离节点的Java程序
1 简介
在此程序中,我们需要找出二叉树中距离最大的节点。根据我们的方法,树的所有节点之间的所有距离都将保持在可变距离内。通过使用变量MaxDistance可以保留具有最大值的距离。最初,MaxDistance初始化为distance的值。如果发现任何大于MaxDistance的值,则覆盖MaxDistance的值。
重复此过程,直到找到树的两个节点之间的最大可能距离。该过程的算法在下面给出。
2 算法思路
- 定义具有三个属性的Node类,即:左和右数据。在此,左代表节点的左子节点,右代表节点的右子节点。
- 创建节点时,数据将传递到该节点的data属性,并且左右都将设置为null。
- 定义另一个具有两个属性root和treeArray的类。
- 根表示树的根节点,并将其初始化为null。
- treeArray将存储二叉树的数组表示形式。
- nodeAtMaxDistance()将找出以最大距离存在的节点:
- 它将计算二叉树中所有节点之间的距离并将其存储在可变距离中。
- MaxDistance跟踪节点之间的最大可能距离。如果maxDistance小于distance,则distance的值将存储在maxDistance中。清除数组以摆脱以前存储的值。最大距离的节点将存储在数组arr中。
- 如果在maxDistance处有一对以上的节点,则将它们存储在数组arr中。
-
convertBTtoArray()将通过遍历二叉树并将元素添加到treeArray来将二叉树转换为其数组表示形式。
getDistance()将计算给定节点到根的距离。
LowestCommonAncestor()将找出节点n1和n2的最低公共祖先。
- 如果任何一个节点都等于根节点,则将root作为最低的公共祖先返回。
- 否则,在左子树和右子树中搜索节点n1和n2。
- 如果找到一个节点,则n1是该节点的左子节点,而n2是该节点的右子节点,反之亦然。返回该节点作为最低公共祖先。
- 首先,它计算每个节点到根节点的距离。
- 从该根节点减去最低共同祖先的2 *距离
3 程序实现
import java.util.ArrayList;
/**
* 一点教程网: http://www.yiidian.com
*/
public class MaxDistance {
//Represent a node of binary tree
public static class Node{
int data;
Node left;
Node right;
public Node(int data){
//Assign data to the new node, set left and right children to null
this.data = data;
this.left = null;
this.right = null;
}
}
//Represent the root of binary tree
public Node root;
int[] treeArray;
int index = 0;
public MaxDistance(){
root = null;
}
//calculateSize() will calculate size of tree
public int calculateSize(Node node)
{
int size = 0;
if (node == null)
return 0;
else {
size = calculateSize (node.left) + calculateSize (node.right) + 1;
return size;
}
}
//convertBTtoArray() will convert binary tree to its array representation
public void convertBTtoArray(Node node) {
//Check whether tree is empty
if(root == null){
System.out.println("Tree is empty");
return;
}
else {
if(node.left != null)
convertBTtoArray(node.left);
//Adds nodes of binary tree to treeArray
treeArray[index] = node.data;
index++;
if(node.right != null)
convertBTtoArray(node.right);
}
}
//getDistance() will find distance between root and a specific node
public int getDistance(Node temp, int n1) {
if (temp != null) {
int x = 0;
if ((temp.data == n1) || (x = getDistance(temp.left, n1)) > 0
|| (x = getDistance(temp.right, n1)) > 0) {
//x will store the count of number of edges between temp and node n1
return x + 1;
}
return 0;
}
return 0;
}
//lowestCommonAncestor() will find out the lowest common ancestor for nodes node1 and node2
public Node lowestCommonAncestor(Node temp, int node1, int node2) {
if (temp != null) {
//If root is equal to either of node node1 or node2, return root
if (temp.data == node1 || temp.data == node2) {
return temp;
}
//Traverse through left and right subtree
Node left = lowestCommonAncestor(temp.left, node1, node2);
Node right = lowestCommonAncestor(temp.right, node1, node2);
//If node temp has one node(node1 or node2) as left child and one node(node1 or node2) as right child
//Then, return node temp as lowest common ancestor
if (left != null && right != null) {
return temp;
}
//If nodes node1 and node2 are in left subtree
if (left != null) {
return left;
}
//If nodes node1 and node2 are in right subtree
if (right != null) {
return right;
}
}
return null;
}
//findDistance() will find distance between two given nodes
public int findDistance(int node1, int node2) {
//Calculates distance of first node from root
int d1 = getDistance(root, node1) - 1;
//Calculates distance of second node from root
int d2 = getDistance(root, node2) - 1;
//Calculates lowest common ancestor of both the nodes
Node ancestor = lowestCommonAncestor(root, node1, node2);
//If lowest common ancestor is other than root then, subtract 2 * (distance of root to ancestor)
int d3 = getDistance(root, ancestor.data) - 1;
return (d1 + d2) - 2 * d3;
}
//nodesAtMaxDistance() will display the nodes which are at maximum distance
public void nodesAtMaxDistance(Node node) {
int maxDistance = 0, distance = 0;
ArrayList<Integer> arr = new ArrayList<>();
//Initialize treeArray
int treeSize = calculateSize(node);
treeArray = new int[treeSize];
//Convert binary tree to its array representation
convertBTtoArray(node);
//Calculates distance between all the nodes present in binary tree and stores maximum distance in variable maxDistance
for(int i = 0; i < treeArray.length; i++) {
for(int j = i; j < treeArray.length; j++) {
distance = findDistance(treeArray[i], treeArray[j]);
//If distance is greater than maxDistance then, maxDistance will hold the value of distance
if(distance > maxDistance) {
maxDistance = distance;
arr.clear();
//Add nodes at position i and j to treeArray
arr.add(treeArray[i]);
arr.add(treeArray[j]);
}
//If more than one pair of nodes are at maxDistance then, add all pairs to treeArray
else if(distance == maxDistance) {
arr.add(treeArray[i]);
arr.add(treeArray[j]);
}
}
}
//Display all pair of nodes which are at maximum distance
System.out.println("Nodes which are at maximum distance: ");
for(int i = 0; i < arr.size(); i = i + 2) {
System.out.println("( " + arr.get(i) + "," + arr.get(i+1) + " )");
}
}
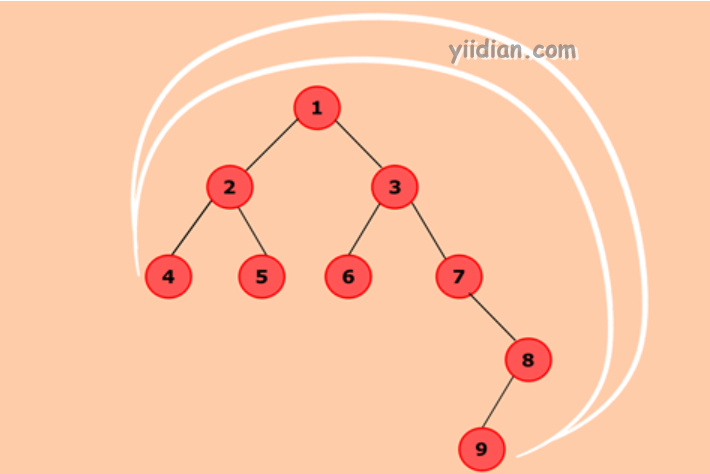
public static void main(String[] args) {
MaxDistance bt = new MaxDistance();
//Add nodes to the binary tree
bt.root = new Node(1);
bt.root.left = new Node(2);
bt.root.right = new Node(3);
bt.root.left.left = new Node(4);
bt.root.left.right = new Node(5);
bt.root.right.left = new Node(6);
bt.root.right.right = new Node(7);
bt.root.right.right.right = new Node(8);
bt.root.right.right.right.left = new Node(9);
//Finds out all the pair of nodes which are at maximum distance
bt.nodesAtMaxDistance(bt.root);
}
}
输出结果为:
Nodes which are at maximum distance:
( 4, 9 )
( 5, 9 )
热门文章
优秀文章


