两个矩阵相减的Java程序

1 说明

在此程序中，我们需要获得两个矩阵相减的结果。

当且仅当它们具有相同的维数，相同的行数和列数时，才能减去两个矩阵A和B。从3×2矩阵中减去2×3矩阵是不可能的。可以通过减去两个矩阵的相应元素来减去两个矩阵。

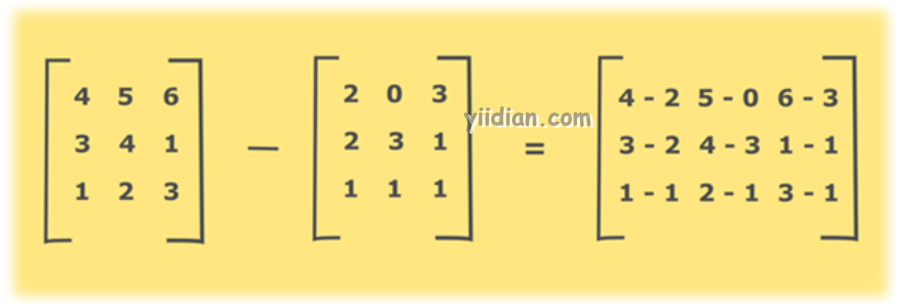
可以通过遍历第一和第二矩阵来执行两个矩阵的减法。计算它们对应元素之间的差异，并将结果存储在第三矩阵中。

2 算法思路

• 步骤1：开始
• 第2步：定义行，列
• 步骤3：初始化第一个矩阵a [] [] = {{4,5,6}，{3,4,1}，{1,2,3}}
• 步骤4：初始化第二个矩阵b [] [] = {{2,0,3}，{2,3,1} {1,1,1}}
• 步骤5：行= a.length
• 步骤6： cols = a [0] .length
• 步骤7：定义diff [] []
• 步骤8：将步骤9重复到步骤10直到i <rows
              // for（i = 0; i <rows; i ++）
• 步骤9：重复步骤10直到j <cols
              // for（j = 0; j <cols; j ++）
• 步骤10： diff [i] [j] = a [i] [j]-b [i] [j]
• 步骤11： 打印“Subtraction of two matrices:”
• 步骤12：将步骤13重复到步骤14，直到i <rows
              // for（i = 0; i <rows; i ++）
• 步骤13：重复步骤14直到j <cols
              // for（j = 0; j <cols; j ++）
• 步骤13：列印diff [i] [j]
• 步骤14：列印新行
• 步骤15：结束

3 程序实现

/**
 * 一点教程网： http://www.yiidian.com
 */
public class Sub_Matrix  
{  
    public static void main(String[] args) {  
        int rows, cols;  
  
        //Initialize matrix a  
          int a[][] = {  
                          {4, 5, 6},  
                          {3, 4, 1},  
                          {1, 2, 3}  
                       };  
  
          //Initialize matrix b  
          int b[][] = {  
                          {2, 0, 3},  
                         {2, 3, 1},  
                         {1, 1, 1}  
                     };  
  
          //Calculates number of rows and columns present in given matrix  
          rows = a.length;  
        cols = a[0].length;  
  
          //Array diff will hold the result  
        int diff[][] = new int[rows][cols];  
  
        //Performs subtraction of matrices a and b. Store the result in matrix diff  
        for(int i = 0; i < rows; i++){  
            for(int j = 0; j < cols; j++){  
                diff[i][j] = a[i][j] - b[i][j];  
            }  
        }  
  
        System.out.println("Subtraction of two matrices: ");  
        for(int i = 0; i < rows; i++){  
            for(int j = 0; j < cols; j++){  
               System.out.print(diff[i][j] + " ");  
            }  
            System.out.println();  
        }  
    }  
}  

 以上代码输出结果为：

Subtraction of two matrices:
1	5    3
1    1    0
0    1    2