判断矩阵是否为恒等矩阵

1 说明

在此程序中，我们需要判断给定的矩阵是否为恒等矩阵。

什么是恒等矩阵

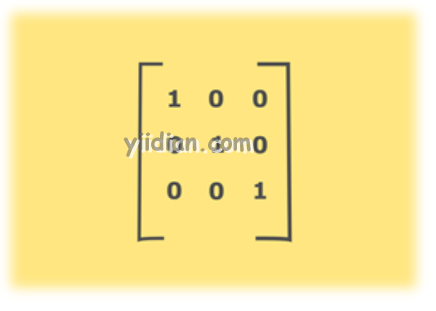
如果矩阵是方形矩阵，则其中对角线的主元素为1，其余元素为零，则称该矩阵为恒等矩阵。

2 算法思路

• 步骤1：开始
• 第2步：定义行，列
• 步骤3： SET标志= true
• 步骤4：初始化矩阵a [] [] = {{1,0,0}，{0,1,0}，{0,0,1}}
• 步骤5：行= a.length
• 步骤6： cols = a [0] .length
• 步骤7： if（rows！= cols）
              则
            打印“矩阵应为方矩阵”，
           否则
         转到步骤8
• 步骤8：将步骤9重复到步骤11，直到i <rows
              // for（i = 0; i <rows; i ++）
• 步骤9：重复步骤10至步骤11直到j <cols
              // for（j = 0; j <cols; j ++）
• 步骤10： if（i == j && a [i] [j] == 1）然后
              SET标志= false
              中断
• 步骤11： if（i！= j && a [i] [j]！= 0）
              SET标志=错误的
              中断
• 步骤12： if（flag）
              then PRINT（“给定矩阵不是一个恒等矩阵”），
              否则为
              PRINT（“给定矩阵不是一个恒等矩阵”）
• 步骤13：结束

3 程序实现

/**
 * 一点教程网： http://www.yiidian.com
 */
public class IdentityMatrix     
{    
    public static void main(String[] args) {    
        int rows, cols;    
        boolean flag = true;    
            
        //Initialize matrix a    
        int a[][] = {       
                        {1, 0, 0},    
                        {0, 1, 0},    
                        {0, 0, 1}    
                    };    
            
        //Calculates the number of rows and columns present in the given matrix    
    
          rows = a.length;    
        cols = a[0].length;    
            
        //Checks whether given matrix is a square matrix or not    
        if(rows != cols){    
            System.out.println("Matrix should be a square matrix");    
        }    
        else {    
            //Checks if diagonal elements are equal to 1 and rest of elements are 0    
            for(int i = 0; i < rows; i++){    
                for(int j = 0; j < cols; j++){    
                  if(i == j && a[i][j] != 1){    
                      flag = false;    
                      break;    
                  }    
                  if(i != j && a[i][j] != 0){    
                      flag = false;    
                      break;    
                  }    
                }    
            }    
                
            if(flag)    
                System.out.println("Given matrix is an identity matrix");    
            else    
                System.out.println("Given matrix is not an identity matrix");    
        }    
    }    
} 

以上代码输出结果为：

Given matrix is an identity matrix