查找二叉树的最大深度和高度的Java程序

1 简介

在此程序中，我们需要找出二叉树的最大高度。二叉树的高度可以定义为根和叶之间的节点数。最大高度将是根与最深叶之间的级别数。为了解决这个问题，我们遍历左子树并计算左子树的高度。同样，通过遍历右子树来计算其高度。最大高度将是左子树和右子树的高度中的最大值。

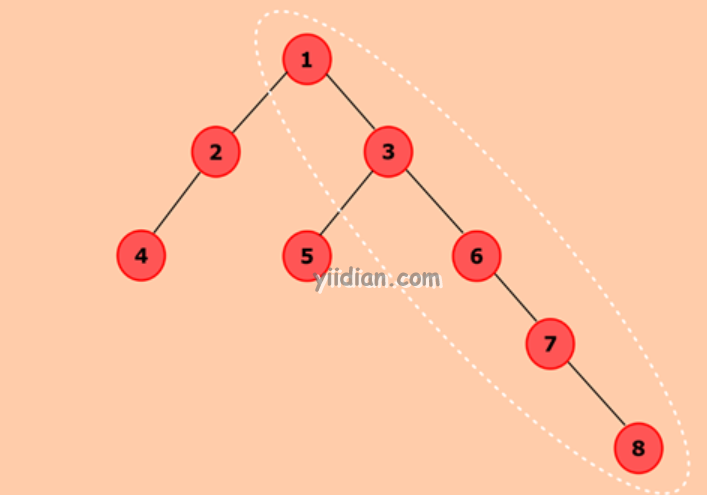
在上面的二叉树中，

左子树的高度为 2 。  
右子树的高度为 4 。  
MaxHeight = Max（leftHeight，rightHeight）+  1 ; 在这里，  1 表示根节点的高度，  
给定的二进制树的最大高度为（4  +  1 ）=  5 由白虚线表示。  

2 算法思路

• 定义具有三个属性的Node类，即：左和右数据。在此，左代表节点的左子节点，右代表节点的右子节点。
• 创建节点时，数据将传递到该节点的data属性，并且左右都将设置为null。
• 定义另一个具有属性根的类。
  • 根表示树的根节点，并将其初始化为null。
• 它检查根是否为空，这意味着树为空。
• 如果树不为空，请遍历左子树以确定左子树的高度，并将值存储在leftHeight中。
• 同样，确定右子树的高度并将其值存储在rightHeight中。
• 最大值将确定leftHeight和rightHeight的最大值，然后为root的高度加1。

3 程序实现

/**
 * 一点教程网： http://www.yiidian.com
 */
public class BinaryTree {  
  
    //Represent the node of binary tree  
    public static class Node{  
        int data;  
        Node left;  
        Node right;  
  
        public Node(int data){  
            //Assign data to the new node, set left and right children to null  
            this.data = data;  
            this.left = null;  
            this.right = null;  
        }  
    }  
  
    //Represent the root of binary tree  
    public Node root;  
    public BinaryTree(){  
        root = null;  
    }  
  
    //findHeight() will determine the maximum height of the binary tree  
    public int findHeight(Node temp){  
        //Check whether tree is empty  
        if(root == null) {  
             System.out.println("Tree is empty");  
            return 0;  
        }  
        else {  
            int leftHeight = 0, rightHeight = 0;  
  
            //Calculate the height of left subtree  
            if(temp.left != null)  
                leftHeight = findHeight(temp.left);  
  
            //Calculate the height of right subtree  
            if(temp.right != null)  
                rightHeight = findHeight(temp.right);  
  
            //Compare height of left subtree and right subtree  
            //and store maximum of two in variable max  
            int max = (leftHeight > rightHeight) ? leftHeight : rightHeight;  
  
            //Calculate the total height of tree by adding height of root  
            return (max + 1);  
        }  
     }  
  
    public static void main(String[] args) {  
  
        BinaryTree bt = new BinaryTree();  
        //Add nodes to the binary tree  
        bt.root = new Node(1);  
        bt.root.left = new Node(2);  
        bt.root.right = new Node(3);  
        bt.root.left.left = new Node(4);  
        bt.root.right.left = new Node(5);  
        bt.root.right.right = new Node(6);  
        bt.root.right.right.right= new Node(7);  
        bt.root.right.right.right.right = new Node(8);  
  
        //Display the maximum height of the given binary tree  
        System.out.println("Maximum height of given binary tree: " + bt.findHeight(bt.root));  
  }  
} 

输出结果为：

Maximum height of given binary tree: 5