查找二叉树最大宽度的Java程序

1 简介

在此程序中，我们需要找出二叉树的最大宽度。二叉树的宽度是任何级别中存在的节点数。因此，具有最大节点数的级别将是二叉树的最大宽度。要解决此问题，请逐级遍历树并计算每个级别中的节点。

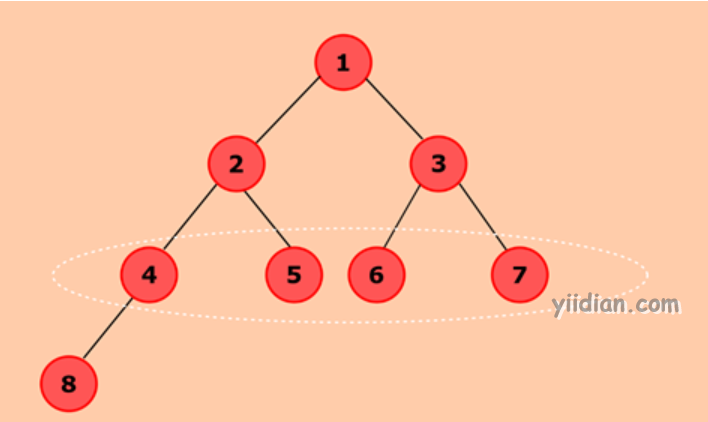
在给定的二叉树中

级别1有一个节点，因此maxWidth =1。
级别2有两个节点，因此maxWidth = 2为（2> 1）。
级别3具有四个节点，因此maxWidth = 4为（4> 2）。
级别4具有一个节点，因此maxWidth = 4为（1 <4）。

因此，上述二叉树的最大宽度为4，用白色椭圆表示。

2 算法思路

• 定义具有三个属性的Node类，即：左和右数据。在此，左代表节点的左子节点，右代表节点的右子节点。
• 创建节点时，数据将传递到该节点的data属性，并且左右都将设置为null。
• 定义另一个具有属性根的类。
  • 根表示树的根节点，并将其初始化为null。
• 变量maxWidth将存储任何级别中存在的最大节点数。
• 该队列用于逐级遍历二叉树。
• 它检查根是否为空，这意味着树为空。
• 如果不是，则将根节点添加到队列中。变量nodesInLevel跟踪每个级别中的节点数。
• 如果nodesInLevel> 0，请从队列的最前面删除该节点，并将其左右子节点添加到队列中。对于第一次迭代，将删除节点1并将其子节点2和3添加到队列中。在第二次迭代中，将删除节点2，将其子级4和5添加到队列中，依此类推。
• MaxWidth将存储max（maxWidth，nodesInLevel）。因此，在任何给定的时间点，它将代表最大的节点数。
• 这将一直持续到遍历树的所有级别为止。

3 程序实现

import java.util.LinkedList;  
import java.util.Queue;  
/**
 * 一点教程网： http://www.yiidian.com
 */  
public class BinaryTree {  
  
      //Represent the node of binary tree  
      public static class Node{  
        int data;  
        Node left;  
        Node right;  
  
        public Node(int data){  
          //Assign data to the new node, set left and right children to null  
          this.data = data;  
          this.left = null;  
          this.right = null;  
        }  
      }  
  
      //Represent the root of binary tree  
      public Node root;  
  
      public BinaryTree(){  
        root = null;  
      }  
  
      //findMaximumWidth() will find out the maximum width of the given binary tree  
      public int findMaximumWidth() {  
          int maxWidth = 0;  
  
          //Variable nodesInLevel keep tracks of number of nodes in each level  
          int nodesInLevel = 0;  
          //queue will be used to keep track of nodes of tree level-wise  
          Queue<Node> queue = new LinkedList<Node>();  
  
          //Check if root is null, then width will be 0  
          if(root == null) {  
              System.out.println("Tree is empty");  
              return 0;  
          }  
          else {  
              //Add root node to queue as it represents the first level  
              queue.add(root);  
  
              while(queue.size() != 0) {  
  
                  //Variable nodesInLevel will hold the size of queue i.e. number of elements in queue  
                  nodesInLevel = queue.size();  
                  //maxWidth will hold maximum width.  
                  //If nodesInLevel is greater than maxWidth then, maxWidth will hold the value of nodesInLevel  
                  maxWidth = Math.max(maxWidth, nodesInLevel);  
  
                  //If variable nodesInLevel contains more than one node  
                  //then, for each node, we'll add left and right child of the node to the queue  
                  while(nodesInLevel > 0) {  
                     Node current = queue.remove();  
                     if(current.left != null)  
                         queue.add(current.left);  
                     if(current.right != null)  
                         queue.add(current.right);  
                     nodesInLevel--;  
                  }  
              }  
          }  
          return maxWidth;  
      }  
  
      public static void main(String[] args) {  
  
          BinaryTree bt = new BinaryTree();  
          //Add nodes to the binary tree  
          bt.root = new Node(1);  
          bt.root.left = new Node(2);  
          bt.root.right = new Node(3);  
          bt.root.left.left = new Node(4);  
          bt.root.left.right = new Node(5);  
          bt.root.right.left = new Node(6);  
          bt.root.right.right = new Node(7);  
          bt.root.left.left.left = new Node(8);  
  
          //Display the maximum width of given tree  
          System.out.println("Maximum width of the binary tree: " + bt.findMaximumWidth());  
      }  
}

输出结果为：

Maximum width of the binary tree: 4