构建二进制搜索树并进行删除和有序遍历的Java程序

1 简介

在此程序中，我们需要创建一个二进制搜索树，从该树中删除一个节点，并通过使用有序遍历遍历该树来显示该树的节点。在有序遍历中，对于给定的节点，首先遍历左子节点，然后遍历根节点，然后遍历右子节点（Left-> Root-> Right）。

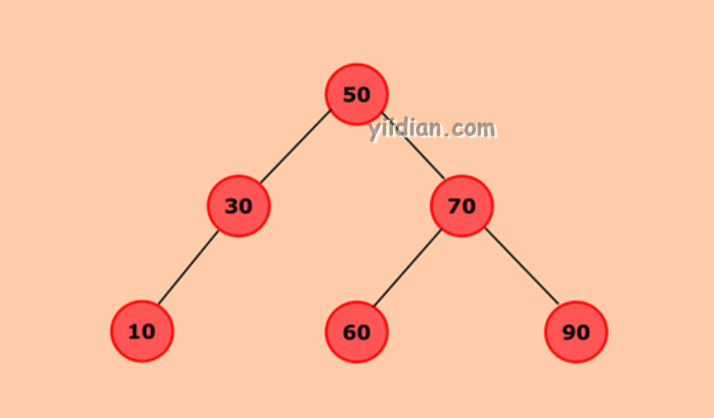
在二叉搜索树中，出现在根左侧的所有节点都将小于根节点，出现在右侧的节点将大于根节点。

插入：

• 如果新节点的值小于根节点，则它将被插入到左子树中。
• 如果新节点的值大于根节点，那么它将被插入到正确的子树中。

删除：

• 如果要删除的节点是叶节点，则该节点的父节点将指向null。例如。如果我们删除90，则父节点70将指向null。
• 如果要删除的节点有一个子节点，则子节点将成为父节点的子节点。例如。如果我们删除30，则剩下的30的子节点10将变成50的左子节点。
• 如果要删除的节点有两个子节点，则从该当前节点的右子树中找到具有最小值的节点（minNode）。当前节点将被其后继节点（minNode）取代。

2 算法思路

• 定义具有三个属性的Node类，即data，left和right。在此，左代表节点的左子节点，右代表节点的右子节点。
• 创建节点时，数据将传递到该节点的data属性，并且left和right都将设置为null。
• 定义另一个具有属性根的类。
  • 根表示树的根节点，并将其初始化为null。
• 它检查root是否为空，这意味着树为空。新节点将成为树的根节点。
• 如果tree不为空，则它将新节点的值与根节点进行比较。如果新节点的值大于根，则新节点将插入到右子树中。否则，它将插入到左子树中。
• 如果要删除的节点的值小于根节点，请在左子树中搜索节点。否则，在右边的子树中搜索。
• 如果找到节点并且它没有子节点，则将节点设置为null。
• 如果节点有一个子节点，则子节点将占据该节点的位置。
• 如果节点有两个子节点，则从其右子树中找到一个最小值节点。此最小值节点将替换当前节点。

3 程序实现

/**
 * 一点教程网： http://www.yiidian.com
 */
public class BinarySearchTree {  
  
    //Represent a node of binary tree  
    public static class Node{  
        int data;  
        Node left;  
        Node right;  
  
        public Node(int data){  
            //Assign data to the new node, set left and right children to null  
            this.data = data;  
            this.left = null;  
            this.right = null;  
        }  
      }  
  
      //Represent the root of binary tree  
      public Node root;  
  
      public BinarySearchTree(){  
          root = null;  
      }  
  
      //insert() will add new node to the binary search tree  
      public void insert(int data) {  
          //Create a new node  
          Node newNode = new Node(data);  
  
          //Check whether tree is empty  
          if(root == null){  
              root = newNode;  
              return;  
            }  
          else {  
              //current node point to root of the tree  
              Node current = root, parent = null;  
  
              while(true) {  
                  //parent keep track of the parent node of current node.  
                  parent = current;  
  
                  //If data is less than current's data, node will be inserted to the left of tree  
                  if(data < current.data) {  
                      current = current.left;  
                      if(current == null) {  
                          parent.left = newNode;  
                          return;  
                      }  
                  }  
                  //If data is greater than current's data, node will be inserted to the right of tree  
                  else {  
                      current = current.right;  
                      if(current == null) {  
                          parent.right = newNode;  
                          return;  
                      }  
                  }  
              }  
          }  
      }  
  
      //minNode() will find out the minimum node  
      public Node minNode(Node root) {  
          if (root.left != null)  
              return minNode(root.left);  
          else  
              return root;  
      }  
  
      //deleteNode() will delete the given node from the binary search tree  
      public Node deleteNode(Node node, int value) {  
          if(node == null){  
              return null;  
           }  
          else {  
              //value is less than node's data then, search the value in left subtree  
              if(value < node.data)  
                  node.left = deleteNode(node.left, value);  
  
              //value is greater than node's data then, search the value in right subtree  
              else if(value > node.data)  
                  node.right = deleteNode(node.right, value);  
  
              //If value is equal to node's data that is, we have found the node to be deleted  
              else {  
                  //If node to be deleted has no child then, set the node to null  
                  if(node.left == null && node.right == null)  
                      node = null;  
  
                  //If node to be deleted has only one right child  
                  else if(node.left == null) {  
                      node = node.right;  
                  }  
  
                  //If node to be deleted has only one left child  
                  else if(node.right == null) {  
                      node = node.left;  
                  }  
  
                  //If node to be deleted has two children node  
                  else {  
                      //then find the minimum node from right subtree  
                      Node temp = minNode(node.right);  
                      //Exchange the data between node and temp  
                      node.data = temp.data;  
                      //Delete the node duplicate node from right subtree  
                      node.right = deleteNode(node.right, temp.data);  
                  }  
              }  
              return node;  
          }  
      }  
  
      //inorder() will perform inorder traversal on binary search tree  
      public void inorderTraversal(Node node) {  
  
          //Check whether tree is empty  
          if(root == null){  
              System.out.println("Tree is empty");  
              return;  
           }  
          else {  
  
              if(node.left!= null)  
                  inorderTraversal(node.left);  
              System.out.print(node.data + " ");  
              if(node.right!= null)  
                  inorderTraversal(node.right);  
  
          }  
      }  
  
      public static void main(String[] args) {  
  
          BinarySearchTree bt = new BinarySearchTree();  
          //Add nodes to the binary tree  
          bt.insert(50);  
          bt.insert(30);  
          bt.insert(70);  
          bt.insert(60);  
          bt.insert(10);  
          bt.insert(90);  
  
          System.out.println("Binary search tree after insertion:");  
          //Displays the binary tree  
          bt.inorderTraversal(bt.root);  
  
          Node deletedNode = null;  
          //Deletes node 90 which has no child  
          deletedNode = bt.deleteNode(bt.root, 90);  
          System.out.println("\nBinary search tree after deleting node 90:");  
          bt.inorderTraversal(bt.root);  
  
          //Deletes node 30 which has one child  
          deletedNode = bt.deleteNode(bt.root, 30);  
          System.out.println("\nBinary search tree after deleting node 30:");  
          bt.inorderTraversal(bt.root);  
  
          //Deletes node 50 which has two children  
          deletedNode = bt.deleteNode(bt.root, 50);  
          System.out.println("\nBinary search tree after deleting node 50:");  
          bt.inorderTraversal(bt.root);  
      }  
}  

输出结果为：

Binary search tree after insertion:
10 30 50 60 70 90 
Binary search tree after deleting node 90:
10 30 50 60 70 
Binary search tree after deleting node 30:
10 50 60 70 
Binary search tree after deleting node 50:
10 60 70